Chapter 10.3, Problem 17AYU

In problems 17-26, find the vertices and foci of each ellipse. Graph each equation by hand. Verify your graph using a graphing utility.

$\frac{x^2}{25}+\frac{y^2}{4}=1$

To determine

(a & b)

To find: Find the vertices and foci of the given equation of the ellipse.

Answer to Problem 17AYU

Solution:

Vertices: $\left(5,0\right)$ and $\left(-5,0\right)$.

Foci: $\left(\surd 21,0\right)$ and $\left(-\surd 21,0\right)$.

Explanation of Solution

Given:

$\frac{x^2}{25}+\frac{y^2}{4}=1$

Formula Used:

Equation	Center	Major axis	Foci	Vertices
$\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ $ a>b>0\text{ and }{b}^2=a^2-c^2$\end{array}$	$\left(0,0\right)$	$x\text{-axis}$	$\left(c,0\right)$	$\left(a,0\right)$
	$\left(0,0\right)$	$x\text{-axis}$	$\left(-c,0\right)$	$\left(-a,0\right)$

Calculation:

The center of the ellipse is at origin $\left(0,0\right)$;

$a=\sqrt{25}=5$; $b=\sqrt{16}=4$

The vertices are $\left(5,0\right)$ and $\left(-5,0\right)$.

To find the value of $c$,

$c²=a²-b²=25-4=21;c=\surd 21$

Hence the foci are $\left(\surd 21,0\right)$ and $\left(-\surd 21,0\right)$.

To determine

c.

To graph: The equation $\frac{x^2}{25}+\frac{y^2}{4}=1$.

Answer to Problem 17AYU

Solution:

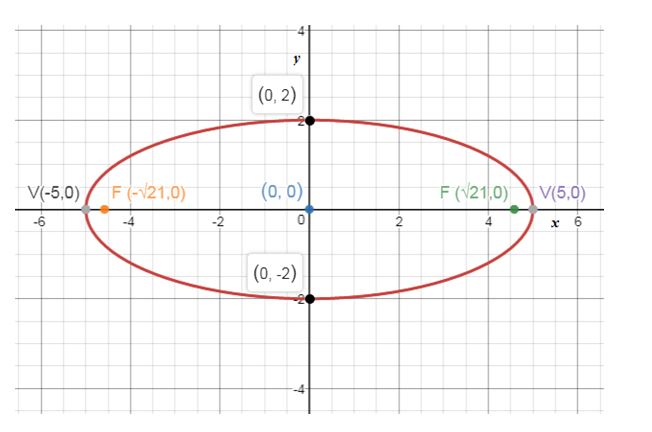
Explanation of Solution

Given:

$\frac{x^2}{25}+\frac{y^2}{4}=1$

Calculation:

The graph of the equation of $\frac{x^2}{25}+\frac{y^2}{4}=1$ is plotted using graphing tool.

Using the given information $\frac{x^2}{25}+\frac{y^2}{4}=1$, we find the $x\text{-intercepts}$ and $y\text{-intercepts}$.

$x\text{-intercepts}$ are $\left(\pm 5, 0\right)$ and $y\text{-intercepts}$ $\left(0,\pm 2\right)$.

Using these points given above, we can plot the points and draw a graph. We find the center $\left(0,0\right)$, focus $\left(\pm \surd 21,0\right)$ and vertex $\left(\pm 5, 0\right)$, We see that the major axis is $x\text{-axis}$. We plot the graph for the equation using the graphing tool to verify it.