Chapter 10.4, Problem 50AYU

In Problems 49-62, find the center, transverse axis, vertices, foci, and asymptotes. Graph each equation by hand. Verify your graph using a graphing utility.

$\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$

To determine

a.

To find: The center, transverse axis, vertices, foci and asymptotes.

Answer to Problem 50AYU

Center: $\left(2,-3\right)$.

Transverse axis: parallel to $y\text{-axis}$.

Vertices: $\left(2,-1\right)$, $\left(2,-5\right)$.

Foci: $\left(2,-3\pm \sqrt{13}\right)$.

Asymptotes: $y+3=\pm \frac{2}{3}\left(x-2\right)$.

Explanation of Solution

Given:

$\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$

Formula used:

Center	Transverse axis	Foci	Vertices	Equation	Asymptotes
$\left(h,k\right)$	Parallel to $y\text{-axis}$	$\left(h,k\pm c\right)$	$\left(h,k\pm a\right)$	$\frac{{\left(y-k\right)}^2}{a^2}-\frac{{\left(x-h\right)}^2}{b^2}=1$; $b^2=c^2-a^2$	$y-k=\pm \frac{a}{b}\left(x-h\right)$

Calculation:

$\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$ is of the form $\frac{{\left(y-k\right)}^2}{a^2}-\frac{{\left(x-h\right)}^2}{b^2}=1$.

$b^2=c^2-a^2$

The center of the hyperbola is $\left(h,k\right)=\left(2,-3\right)$; $h=2, k=-3$.

$a=2, b=3$

Vertices: $\left(h,k\pm a\right)=\left(2,-3\pm 2\right)=\left(2,-1\right),\left(2,-5\right)$.

$c^2=3^2+2^2=\surd 13$

Foci: $\left(h,k\pm c\right)=\left(2,-3\pm \sqrt{13}\right)$.

From the given data we see that, transverse axis is parallel to $y\text{-axis}$.

Asymptotes: $y+3=\pm \frac{2}{3}\left(x-2\right)$.

To determine

b.

To graph: The equation $\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$.

Answer to Problem 50AYU

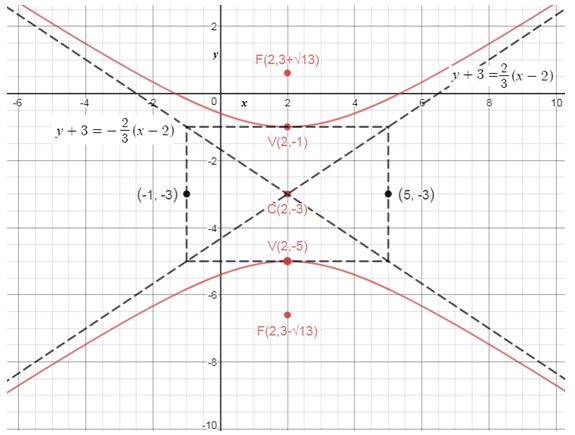
Explanation of Solution

Given:

$\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$

Graph:

The graph of the equation of $\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$ is plotted.

Using the given equation $\frac{{\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$. We find the Center at $\left(2,-3\right)$; Foci: $\left(2,-3\pm \sqrt{13}\right)$, Vertices: $\left(2,-1\right)$, $\left(2,-5\right)$, Asymptotes: $y+3=\pm \frac{2}{3}\left(x-2\right)$.

Transverse axis is parallel to $y\text{-axis}$. We find, $a=2$, $b=3$. With the information available we plot the graph of $\frac{ {\left(y+3\right)}^2}{4}-\frac{{\left(x-2\right)}^2}{9}=1$ and verify the same using the graphing tool.