To determine To find: a. The rectangular equation of the trajectory and identify the curve. Answer a. y = x tan θ − 16 x 2 v o 2 cos ² θ Explanation Given: The position of a projectile fired with an initial velocity v 0 feet per second and at an angle θ to the horizontal at the end of t seconds is given by the parametric equations. x = ( v 0 cos θ ) t , y = ( v 0 sin θ ) t − 16 t ² Formula used: x = ( v o cos θ ) t , y = − 1 2 g t ² + ( v o sin θ ) t + h Calculation: a. x = ( v 0 cos θ ) t , y = ( v 0 sin θ ) t − 16 t ² t = x / v o cos θ y = ( v o sin θ ) ( x v o cos θ ) − 16 ( x v o cos θ ) ² y = x tan θ − 16 ( x v o cos θ ) ² y = x tan θ − 16 x 2 v o 2 cos ² θ y is a quadratic function of x and it represents the graph of a parabola where a = − 16 v o 2 cos θ , b = tan θ and c = 0 . To determine To find: b. To show that the projectile hits the ground ( y = 0 ) when t = 1 / 16 v o sin θ . Answer b. t = v o sin θ 16 Explanation Given: The position of a projectile fired with an initial velocity v 0 feet per second and at an angle θ to the horizontal at the end of t seconds is given by the parametric equations. x = ( v 0 cos θ ) t , y = ( v 0 sin θ ) t − 16 t ² Formula used: x = ( v o cos θ ) t , y = − 1 2 g t ² + ( v o sin θ ) t + h Calculation: b. y = 0 y = ( v o sin θ ) t − 16 t ² = 0 t ( ( v o sin θ ) − 16 t ) = 0 t = v o sin θ 16 To determine To find: c. How far has the projectile traveled (horizontally) when it strikes the ground? In other words, find the range R. Answer c. x = v o ² sin 2 θ / 32 Explanation Given: The position of a projectile fired with an initial velocity v 0 feet per second and at an angle θ to the horizontal at the end of t seconds is given by the parametric equations. x = ( v 0 cos θ ) t , y = ( v 0 sin θ ) t − 16 t ² Formula used: x = ( v o cos θ ) t , y = − 1 2 g t ² + ( v o sin θ ) t + h Calculation: c. To find R We substitute t in x x = ( v o cos θ ) t x = ( v o cos θ ) v o sin θ 16 x = v o ² cos θ sin θ / 16 x = v o ² sin 2 θ / 32 To determine To find: d. Find the time t when x = y . Then find the horizontal distance x and the vertical distance y traveled by the projectile in this time. Then compute √ x ² + y ² . This is the distance R, the range, that the projectile travels up a plane inclined at 45 ° to the horizontal ( x = y ) . Answer d. x ² + y 2 = √ 2 ( ( v o 2 cos θ 16 ) ( sin θ − cos θ ) ) θ > 45 as sin θ − cos θ > 0 Explanation Given: The position of a projectile fired with an initial velocity v 0 feet per second and at an angle θ to the horizontal at the end of t seconds is given by the parametric equations. x = ( v 0 cos θ ) t , y = ( v 0 sin θ ) t − 16 t ² Formula used: x = ( v o cos θ ) t , y = − 1 2 g t ² + ( v o sin θ ) t + h Calculation: d. x = y ( v o cos θ ) t = ( v o sin θ ) t − 16 t ² 16 t ² + ( v o cos θ ) t − ( v o sin θ ) t = 0 t ( 16 t + ( v o cos θ ) − ( v o sin θ ) ) = 0 t = 0 ; t = v o sin θ − v o cos θ 16 At t = v o sin θ − v o cos θ 16 x = ( v o cos θ ) v o sin θ − v o cos θ 16 = ( v o 2 cos θ 16 ) ( sin θ − cos θ ) x = y hence, y = ( v o 2 − cos ² θ + sin θ cos θ 16 ) x ² + y 2 = √ 2 ( ( v o 2 cos θ 16 ) ( sin θ − cos θ ) ) θ > 45 as sin θ − cos θ > 0

Precalculus Enhanced with Graphing Utilities

6th Edition

ISBN: 9780321795465

Author: Michael Sullivan, Michael III Sullivan

Publisher: PEARSON

See similar textbooks

Videos

Textbook Question

Chapter 10.7, Problem 60AYU

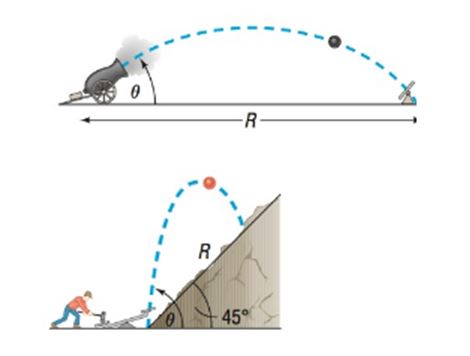
Projectile Motion The position of a projectile fired with an initial velocity $υ_{0}$ feet per second and at an angle $θ$ to the horizontal at the end of $t$ seconds is given by the parametric equations

$x = (υ_{0} \cos θ) t$ $y = (υ_{0} \sin θ) t - 16 t^{2}$

See the illustration.

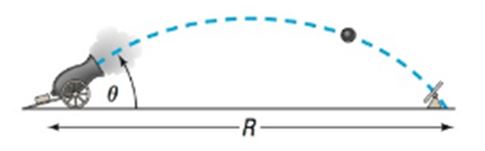
Chapter 10.7, Problem 60AYU, Projectile Motion The position of a projectile fired with an initial velocity 0 feet per second and , example 1

a. Obtain the rectangular equation of the trajectory and identify the curve.

b. Show that the projectile hits the ground $(y = 0)$ when $t = \frac{1}{16} υ_{0} \sin θ$ .

c. How far has the projectile traveled (horizontally) when it strikes the ground? In other words, find the range $R$ .

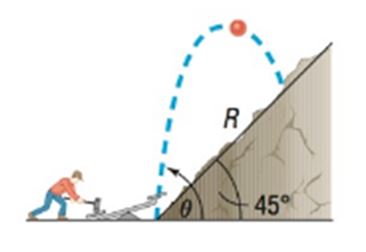
d. Find the time $t$ when $x = y$ . Then find the horizontal distance $x$ and the vertical distance $y$ traveled by the projectile in this time. Then compute $\sqrt{x^{2} + y^{2}}$ . This is the distance $R$ , the range, that the projectile travels up a plane inclined at $45^{\circ}$ to the horizontal $(x = y)$ . See the following illustration. (See also Problem 99 in Section 7.6.)

Chapter 10.7, Problem 60AYU, Projectile Motion The position of a projectile fired with an initial velocity 0 feet per second and , example 2

Expert Solution

To determine

To find:

a. The rectangular equation of the trajectory and identify the curve.

Answer to Problem 60AYU

a. $y = x tan θ - \frac{16 x^{2}}{v_{o}^{2} \cos ² θ}$

Explanation of Solution

Given:

The position of a projectile fired with an initial velocity $v_{0}$ feet per second and at an angle $θ$ to the horizontal at the end of $t$ seconds is given by the parametric equations.

$x = (v_{0} cos θ) t$ , $y = (v_{0} sin θ) t - 16 t ²$

Precalculus Enhanced with Graphing Utilities, Chapter 10.7, Problem 60AYU , additional homework tip 1

Formula used:

$x = (v_{o} cos θ) t$ , $y = - \frac{1}{2} g t ² + (v_{o} sin θ) t + h$

Calculation:

a. $x = (v_{0} cos θ) t$ , $y = (v_{0} sin θ) t - 16 t ²$

$t = x / v_{o} cos θ$

$y = (v_{o} sin θ) (\frac{x}{v_{o} cos θ}) - 16 (\frac{x}{v_{o} cos θ}) ²$

$y = x tan θ - 16 (\frac{x}{v_{o} cos θ}) ²$

$y = x tan θ - \frac{16 x^{2}}{v_{o}^{2} \cos ² θ}$

$y$ is a quadratic function of $x$ and it represents the graph of a parabola where $a = - \frac{16}{v_{o}^{2} \cos θ}$ , $b = tan θ$ and $c = 0$ .

Expert Solution

To determine

To find:

b. To show that the projectile hits the ground $(y = 0)$ when $t = 1 / 16 v_{o} sin θ$ .

Answer to Problem 60AYU

b. $t = \frac{v_{o} sin θ}{16}$

Explanation of Solution

Given:

The position of a projectile fired with an initial velocity $v_{0}$ feet per second and at an angle $θ$ to the horizontal at the end of $t$ seconds is given by the parametric equations.

$x = (v_{0} cos θ) t$ , $y = (v_{0} sin θ) t - 16 t ²$

Precalculus Enhanced with Graphing Utilities, Chapter 10.7, Problem 60AYU , additional homework tip 2

Formula used:

$x = (v_{o} cos θ) t$ , $y = - \frac{1}{2} g t ² + (v_{o} sin θ) t + h$

Calculation:

b. $y = 0$

$y = (v_{o} sin θ) t - 16 t ² = 0$

$t ((v_{o} sin θ) - 16 t) = 0$

$t = \frac{v_{o} sin θ}{16}$

Expert Solution

To determine

To find:

c. How far has the projectile traveled (horizontally) when it strikes the ground? In other words, find the range R.

Answer to Problem 60AYU

c. $x = v_{o} ² sin 2 θ / 32$

Explanation of Solution

Given:

The position of a projectile fired with an initial velocity $v_{0}$ feet per second and at an angle $θ$ to the horizontal at the end of $t$ seconds is given by the parametric equations.

$x = (v_{0} cos θ) t$ , $y = (v_{0} sin θ) t - 16 t ²$

Precalculus Enhanced with Graphing Utilities, Chapter 10.7, Problem 60AYU , additional homework tip 3

Formula used:

$x = (v_{o} cos θ) t$ , $y = - \frac{1}{2} g t ² + (v_{o} sin θ) t + h$

Calculation:

c. To find R

We substitute $t$ in $x$

$x = (v_{o} cos θ) t$

$x = (v_{o} cos θ) \frac{v_{o} sin θ}{16}$

$x = v_{o} ² cos θ sin θ / 16$

$x = v_{o} ² sin 2 θ / 32$

Expert Solution

To determine

To find:

d. Find the time $t$ when $x = y$ . Then find the horizontal distance $x$ and the vertical distance $y$ traveled by the projectile in this time. Then compute $\sqrt x ² + y ²$ . This is the distance R, the range, that the projectile travels up a plane inclined at $45 °$ to the horizontal $(x = y)$ .

Answer to Problem 60AYU

d. $\sqrt{x ² + y^{2}} = \sqrt 2 ((\frac{v_{o}^{2} \cos θ}{16}) (sin θ - cos θ))$ $θ > 45$ as $sin θ - cos θ > 0$

Explanation of Solution

Given:

The position of a projectile fired with an initial velocity $v_{0}$ feet per second and at an angle $θ$ to the horizontal at the end of $t$ seconds is given by the parametric equations.

$x = (v_{0} cos θ) t$ , $y = (v_{0} sin θ) t - 16 t ²$

Precalculus Enhanced with Graphing Utilities, Chapter 10.7, Problem 60AYU , additional homework tip 4

Formula used:

$x = (v_{o} cos θ) t$ , $y = - \frac{1}{2} g t ² + (v_{o} sin θ) t + h$

Calculation:

d. $x = y$

$(v_{o} cos θ) t = (v_{o} sin θ) t - 16 t ²$

$16 t ² + (v_{o} cos θ) t - (v_{o} sin θ) t = 0$

$t (16 t + (v_{o} cos θ) - (v_{o} sin θ)) = 0$

$t = 0$ ; $t = \frac{v_{o} sin θ - v_{o} cos θ}{16}$

At $t = \frac{v_{o} sin θ - v_{o} cos θ}{16}$

$x = (v_{o} cos θ) \frac{v_{o} sin θ - v_{o} cos θ}{16} = (\frac{v_{o}^{2} cos θ}{16}) (sin θ - cos θ)$

$x = y$ hence,

$y = (\frac{v_{o}^{2} - \cos ² θ + sin θ cos θ}{16})$

$\sqrt{x ² + y^{2}} = \sqrt 2 ((\frac{v_{o}^{2} \cos θ}{16}) (sin θ - cos θ))$ $θ > 45$ as $sin θ - cos θ > 0$

Chapter 10.7, Problem 59AYU

Chapter 10.7, Problem 61AYU

Chapter 10 Solutions

Precalculus Enhanced with Graphing Utilities

Ch. 10.2 - The formula for the distance d from P 1 =( x 1 , y...Ch. 10.2 - To complete the square of x 2 4x , add_______...Ch. 10.2 - Use the Square Root Method to find the real...Ch. 10.2 - The point that is symmetric with respect to the...Ch. 10.2 - To graph y= ( x3 ) 2 +1 , shift the graph of y= x...Ch. 10.2 - Prob. 6AYU Ch. 10.2 - Prob. 7AYU Ch. 10.2 - Prob. 8AYU Ch. 10.2 - Prob. 9AYU Ch. 10.2 - Prob. 10AYU

Additional Math Textbook Solutions

Find more solutions based on key concepts

CHECK POINT 1 In a survey on musical tastes, respondents were asked: Do you listed to classical music? Do you l...

Thinking Mathematically (6th Edition)

Derivative Calculations In Exercises 1–8, given y = f(u) and u = g(x), find dy/dx = dy/dx = f′(g(x))g′(x). 1. y...

University Calculus: Early Transcendentals (4th Edition)

Assessment 1-1A How many triangles are in the following figure?

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

In Exercises 13–16, find the margin of error for the values of c, ?, and n. 13. c = 0.95, ? = 5.2, n = 30

Elementary Statistics: Picturing the World (7th Edition)

Calculating derivatives Find dy/dx for the following functions. 21. y = x sin x

Calculus: Early Transcendentals (2nd Edition)

1. combination of numbers, variables, and operation symbols is called an algebraic______.

Algebra and Trigonometry (6th Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.