Chapter 10.7, Problem 58AYU

Uniform Motion A Cessna (heading south at 120 mph) and a Boeing 747 (heading west at 600 mph) are flying toward the same point at the same altitude. The Cessna is 100 miles from the point where the flight patterns intersect, and the 747 is 550 miles from this intersection point. See the figure.

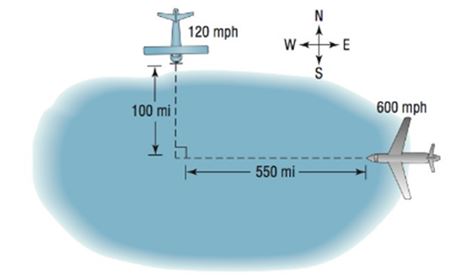
a. Find parametric equations that model the motion of the Cessna and the 747.

b. Find a formula for the distance between the planes as a function of time.

c. Graph the function in part (b) using a graphing utility.

d. What is the minimum distance between the planes? When are the planes closest?

e. Simulate the motion of the planes by simultaneously graphing the equations found in part (a).

To determine

To find:

a. parametric equations that model the motion of the Cessna and the 747.

Answer to Problem 58AYU

a. Boeing 747: $x = -600t + 550$ $y = 0$; Cessna: $x = 0$, $y = -120t + 100$

Explanation of Solution

Given:

A Cessna (heading south at 120 mph) and a Boeing 747 (heading west at 600 mph) are flying toward the same point at the same altitude. The Cessna is 100 miles from the point where the flight patterns intersect, and the 747 is 550 miles from this intersection point.

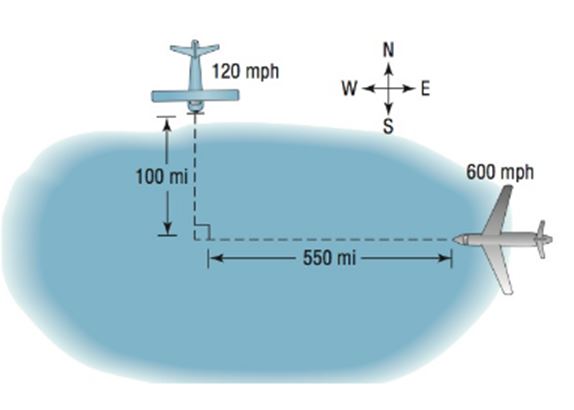
Calculation:

a. At $t = 0$,

Cessna is at a distance of 100 miles from intersection and is travelling south $(y\text{-axis})$ at a speed of 120 mph.

Parametric equation for Cessna:

$x = 0$, $y = -120t + 100$

At $t = 0$,

Boeing 747 is 550 miles from the intersection and is travelling west $(x\text{-axis})$ at a speed of 600mph.

Parametric equation for Boeing 747:

$x = -600t + 550$, $y = 0$

To determine

To find:

b. A formula for the distance between the planes as a function of time.

Answer to Problem 58AYU

b. $d = \sqrt{\left(-600t + 550\right)² + {\left(-120t + 100\right)}^2}$

Explanation of Solution

Given:

A Cessna (heading south at 120 mph) and a Boeing 747 (heading west at 600 mph) are flying toward the same point at the same altitude. The Cessna is 100 miles from the point where the flight patterns intersect, and the 747 is 550 miles from this intersection point.

Calculation:

b. As per the given figure we can use Pythagoras theorem to find the distance $d$ in terms of $t$

$d = \sqrt{\left(-600t + 550\right)² + {\left(-120t + 100\right)}^2}$

To determine

To find:

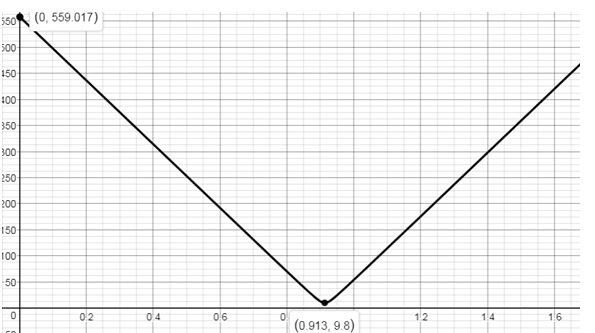
c. Graph the function in part (b) using a graphing utility.

Answer to Problem 58AYU

c.

Explanation of Solution

Given:

A Cessna (heading south at 120 mph) and a Boeing 747 (heading west at 600 mph) are flying toward the same point at the same altitude. The Cessna is 100 miles from the point where the flight patterns intersect, and the 747 is 550 miles from this intersection point.

Calculation:

c. Graph the function in part c

To determine

To find:

d. What is the minimum distance between the planes? When are the planes closest? Simulate the motion of the planes by simultaneously graphing the equations found in part (a).

Answer to Problem 58AYU

d. Distance between the cars is $9.8$ miles. At $0.913$ hours, the cars are closer to each other.

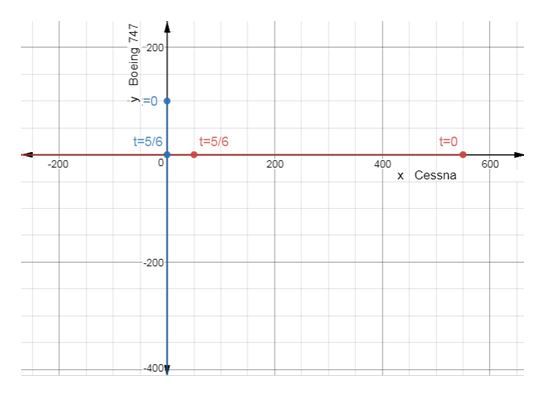
Explanation of Solution

Given:

A Cessna (heading south at 120 mph) and a Boeing 747 (heading west at 600 mph) are flying toward the same point at the same altitude. The Cessna is 100 miles from the point where the flight patterns intersect, and the 747 is 550 miles from this intersection point.

Calculation:

d. From the graph above the minimum distance between the planes is $9.8$ miles. At $0.913$ hours, the planes are closer to each other.