Chapter 10.2, Problem 28AYU

In Problems 21-38, find the equation of the parabola described. Find the two points that define the latus rectum, and graph the equation by hand.

Vertex at $\left(0,\text{ 0}\right)$; axis of symmetry the $x\text{-axis}$; containing the point $\left(2,\text{ 3}\right)$

To determine

(a & b)

The equation of the parabola described and two points that define the latus rectum for the following description.

Vertex at $\left(0,0\right)$; axis of symmetry the $x\text{-axis}$; containing the point $\left(2,3\right)$.

Answer to Problem 28AYU

$y^2=\frac{4}{3}x$, Latus rectum: $\left(\frac{1}{3},\frac{2}{3}\right)$ and $\left(\frac{1}{3},\frac{-2}{3}\right)$.

Explanation of Solution

Given:

Vertex at $\left(0,0\right)$; axis of symmetry the $x\text{-axis}$; containing the point $\left(2,3\right)$.

Formula used:

Vertex	Focus	Directrix	Equation	Description
$\left(0,0\right)$	$\left(a,0\right)$	$x=-a$	$y^2=4ax$	Parabola, axis of symmetry is $x\text{-axis}$, opens right

Calculation:

The vertex $V\left(0,0\right)$ and the axis of symmetry is $x\text{-axis}$, hence the parabola opens right or left. But it is given that axis of symmetry contains $\left(2,3\right)$ and it is right of $\left(0,0\right)$. Hence the parabola opens right. Hence the equation has the form $y^2=4ax$.

Substituting $\left(2,3\right)$ in the equation $y^2=4*a*x$ we get,

$4=4a\left(3\right)$

$a=\frac{1}{3}$

Hence, the focus is $\left(\frac{1}{3},0\right)$.

The equation of the parabola is $y^2=\frac{4}{3}x$.

To find the points that define the latus rectum, Let $x=\frac{1}{3}$ in the above equation.

We get,

$y^2=\frac{4}{3}*\frac{1}{3}$

$y=\pm \frac{2}{3}$

Hence $\left(\frac{1}{3},\frac{2}{3}\right)$ and $\left(\frac{1}{3},\frac{-2}{3}\right)$ defines the latus rectum.

To determine

c.

To graph: The parabola for the equation $y^2=\frac{4}{3}x$.

Answer to Problem 28AYU

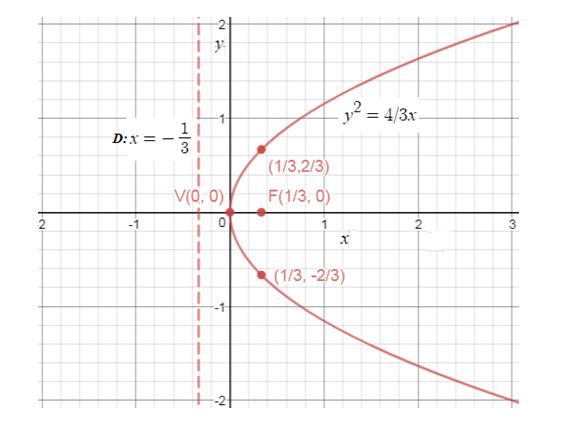
Explanation of Solution

Given:

Vertex at $\left(0,0\right)$; axis of symmetry the $x\text{-axis}$; containing the point $\left(2,3\right)$.

Calculation:

The graph of the parabola $y^2=\frac{4}{3}x$.

Using the given information $V\left(0,0\right)$ and the point $\left(2,3\right)$ that passes through the axis symmetry the $x\text{-axis}$, we find $F\left(\frac{1}{3},0\right)$ and we have formed the equation and plotted the graph for $y^2=\frac{4}{3}x$. The focus $F\left(\frac{1}{3},0\right)$ and the vertex $V\left(0,0\right)$ lie on the horizontal line $x=\text{ 0}$ as shown.

The equation for directrix D: $x=-\frac{1}{3}$ is shown as dotted line. The parabola opens to the right. The points $\left(\frac{1}{3},\frac{2}{3}\right)$ and $\left(\frac{1}{3},\frac{-2}{3}\right)$ defines the latus rectum.