Chapter 10.4, Problem 70AYU

To determine

To find: Analyze the equation.

Answer to Problem 70AYU

The equation represents parabola.

Explanation of Solution

Given:

$y²=-12\left(x+1\right)$

Formula used:

Vertex	Focus	Directrix	Equation	Description
$\left(h,k\right)$	$\left(h-a,0\right)$	$x=h+a$	${\left(y-k\right)}^2=-4a\left(x-h\right)$	Parabola, axis of symmetry is parallel to $x\text{-axis}$, opens left

Calculation:

Given that $y²=-12\left(x+1\right)$.

The equation represents parabola.

The axis of symmetry is parallel to $x\text{-axis}$.

$V\left(h,k\right)=\left(\mathrm{-1},0\right)$

Hence, $h=\mathrm{-1},k=0$

For $a=3$,

$F\left(h-a,k\right)=F\left(-4,0\right)$

The coordinates of the focus is $F\left(\mathrm{-4},0\right)$.

Directrix: $x=-1+3=2$.

The graph of the equation of $y²=-12\left(x+1\right)$ is plotted.

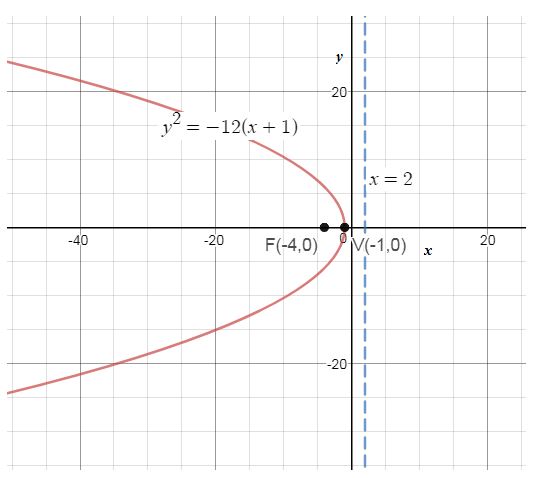
Using the given equation $y²=-12\left(x+1\right)$, we plot the graph using graphing tool.

The graph represents a parabola, with vertex $\left(\mathrm{-1},0\right)$, directrix $x=2$ and the axis of symmetry is parallel to $x\text{-axis}$, opens left.