Chapter 10.7, Problem 52AYU

Catching a Bus Jodi’s bus leaves at 5:30 PM and accelerates at the rate of 3 meters per second per second. Jodi, who can run 5 meters per second, arrives at the bus station 2 seconds after the bus has left and runs for the bus.

a. Find parametric equations that model the motions of the bus and Jodi as a function of time.

[Hint: The position $s$ at time $t$ of an object having acceleration a is $s=\frac{1}{2}a{t}^2$.]

b. Determine algebraically whether Jodi will catch the bus. If so, when?

c. Simulate the motion of the bus and Jodi by simultaneously graphing the equations found in part (a).

To determine

To find:

a. Parametric equations that model the motions of the bus and Jodi as a function of time. [Hint: The position s at time $t$ of an object having acceleration as is $s=1/2at²$].

Answer to Problem 52AYU

a. $\left(1.5t², 1\right)$, $\left(5\left(t - 2\right), 5\right)$

Explanation of Solution

Given:

Jodi’s bus leaves at 5:30 pm and accelerates at the rate of 3 meters per second per second. Jodi, who can run 5 meters per second, arrives at the bus station 2 seconds after the bus has left and runs for the bus.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be bus’s path and $y_2 = 5$ be Jodi’s path.

a. Bus: $x_1 = \frac{1}{2}\left(3\right)t² = 1.5t²$

$y_1 = 1$

Jodi:

$x_2 = 5\left(t - 2\right)$

$y_2 = 5$

To determine

To find:

b. Algebraically whether Jodi will catch the bus. If so, when?

Answer to Problem 52AYU

b. No, Jodi cannot catch the bus.

Explanation of Solution

Given:

Jodi’s bus leaves at 5:30 pm and accelerates at the rate of 3 meters per second per second. Jodi, who can run 5 meters per second, arrives at the bus station 2 seconds after the bus has left and runs for the bus.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be bus’s path and $y_2 = 5$ be Jodi’s path.

b.Bill will catch the train only when $x_1 = x_2$

$1.5t² = 5\left(t - 2\right)$

$1.5t² - 5t + 10 = 0$

$t$ does not have any real function as $b² - 4ac = 25 - 4 \&*\#x00A0;10 \&*\#x00A0;1.5 = -35 < 0$

Hence Jodi cannot catch the Bus.

To determine

To find:

c. Simulate the motion of the bus and Jodi by simultaneously graphing the equations found in part (a).

Answer to Problem 52AYU

c.

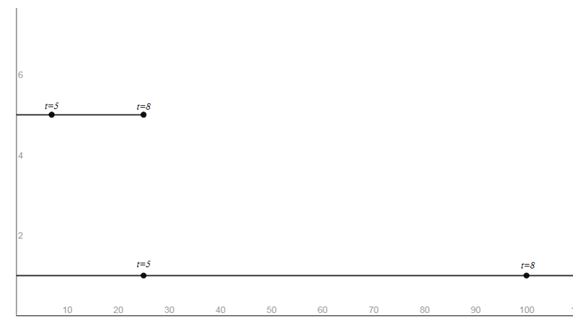
Explanation of Solution

Given:

Jodi’s bus leaves at 5:30 pm and accelerates at the rate of 3 meters per second per second. Jodi, who can run 5 meters per second, arrives at the bus station 2 seconds after the bus has left and runs for the bus.

Formula used:

$s = \frac{1}{2}at²$

Calculation:

Let $y_1 = 1$ be bus’s path and $y_2 = 5$ be Jodi’s path.

c.