Chapter 10.7, Problem 55AYU

Projectile Motion Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of ${45}^{\circ }$ to the horizontal.

a. Find parametric equations that model the position of the ball as a function of time.

b. How long is the ball in the air?

c. Determine the horizontal distance that the ball travels.

d. When is the ball at its maximum height? Determine the maximum height of the ball.

e. Using a graphing utility, simultaneously graph the equations found in part (a).

To determine

To find:

a. Parametric equations that model the position of the ball as a function of time.

Answer to Problem 55AYU

a. $x=20\surd 2t$, $y=-4.9t^2 + 20\sqrt{2}t + 300$

Explanation of Solution

Given:

Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of $45°$ to the horizontal.

Formula used:

$x=\left(v_o\text{cos}\theta \right)t$, $y=-\frac{1}{2}gt² + \left(v_o\text{sin}\theta \right)t + h$

Calculation:

$v_o=40$, $\theta =45°$

a. $x=\left(40\text{cos}45\right)t$

$x=\left(40 \&*\#x00A0;\frac{1}{\sqrt{2}}\right)t=20\surd 2t$

$h=300$

$y=-\frac{1}{2} \&*\#x00A0;9.8t² + (40\sin 45)t + 300$

$y=-4.9t² + 40t\text{sin}45 + 300$

$y=-4.9t^2 + 20\sqrt{2}t + 300$

To determine

To find:

b. How long is the ball in the air?

Answer to Problem 55AYU

b. $11.23$ secconds.

Explanation of Solution

Given:

Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of $45°$ to the horizontal.

Formula used:

$x=\left(v_o\text{cos}\theta \right)t$, $y=-\frac{1}{2}gt² + \left(v_o\text{sin}\theta \right)t + h$

Calculation:

$v_o=40$, $\theta =45°$

b. The ball is in the air until $y=0$, Solve:

$y=-4.9t² + 20\sqrt{2}t + 300$

$0=-4.9t^2 + 20\sqrt{2}t + 300$

$t=\frac{-20\surd 2 \pm \sqrt{{\left(20\surd 2\right)}^2 - 4\left(-4.9\right)\left(300\right)}}{2\left(-4.9\right)}$

$t=-5.45$ or $11.23$

The ball is in the air for $11.23$ seconds.

To determine

To find:

c. The horizontal distance that the ball travels.

Answer to Problem 55AYU

c. $317.63$ meters.

Explanation of Solution

Given:

Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of $45°$ to the horizontal.

Formula used:

$x=\left(v_o\text{cos}\theta \right)t$, $y=-\frac{1}{2}gt² + \left(v_o\text{sin}\theta \right)t + h$

Calculation:

$v_o=40$, $\theta =45°$

c. Horizontal distance $x=\left(v_o\text{cos}\theta \right)t$

$x=20\surd 2 \&*\#x00A0;11.23 \approx 317.63$ meters.

To determine

To find:

d. When is the ball at its maximum height? Determine the maximum height of the ball.

Answer to Problem 55AYU

d. $y \approx 340.82$ metres.

Explanation of Solution

Given:

Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of $45°$ to the horizontal.

Formula used:

$x=\left(v_o\text{cos}\theta \right)t$, $y=-\frac{1}{2}gt² + \left(v_o\text{sin}\theta \right)t + h$

Calculation:

$v_o=40$, $\theta =45°$

d. The maximum height is at vertex of the quadratic function.

$t=-\frac{b}{2a}=- \frac{20\surd 2}{2\left(-4.9\right)} \approx 2.89$ seconds.

Substituting the value in $y=-4.9t² + 20\sqrt{2}t + 300$

$y=-4.9\left(2.89\right)² + 20\sqrt{2}\left(2.89\right) + 300$

$y \approx 340.82$ metres.

To determine

To find:

e. Using a graphing utility, simultaneously graph the equations found in part (a).

Answer to Problem 55AYU

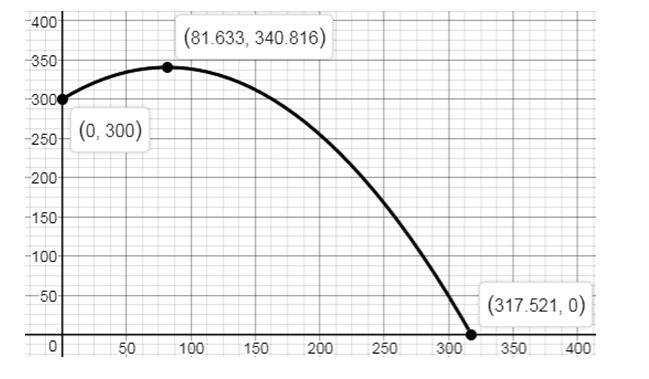
Explanation of Solution

Given:

Suppose that Adam hits a golf ball off a cliff 300 meters high with an initial speed of 40 meters per second at an angle of $45°$ to the horizontal.

Formula used:

$x=\left(v_o\text{cos}\theta \right)t$, $y=-\frac{1}{2}gt² + \left(v_o\text{sin}\theta \right)t + h$

Calculation:

$v_o=40$, $\theta =45°$

e. Graph of the equation found in a.