Chapter 10.4, Problem 78AYU

An Explosion Two recording devices are set 2400 feet apart, with the device at point $A$ to the west of the device at point $B$. At a point between the devices 300 feet from point $B$, a small amount of explosive is detonated. The recording devices record the time until the sound reaches each. How far directly north of point $B$ should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation?

To determine

How far directly north of point $\text{B}$ should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation?

Answer to Problem 78AYU

Solution:

700 feet.

Explanation of Solution

Given:

Two recording devices are set 2400 feet apart, with the device at point $\text{A}$ to the west of the device at point $\text{B}$. At a point between the devices 300 feet from point $\text{B}$, a small amount of explosive is detonated. The recording devices record the time until the sound reaches each.

Formula used:

Equation of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, $b^2=c^2-a^2$.

Calculation:

Set of all points where explosion takes place and the time difference is same, forms a hyperbola with $\text{A}$ and $\text{B}$ as the foci.

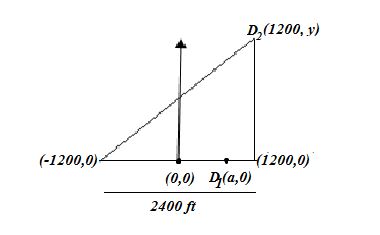
Since $\text{A}$ and $\text{B}$ are foci we have, $2c=2400$, $c=1200$.

$D_1$ is on the transverse axis and is on the hyperbola. Hence $D_1$ is the vertex of the hyperbola.

Since it is 300 feet from $\text{B}$, $a=2400-300=900$.

The equation of the hyperbola is,

$\frac{x^2}{810000}-\frac{y^2}{63000}=1$

The point $\left(1200,y\right)$ lies on the hyperbola.

$\frac{{1200}^2}{810000}-\frac{y^2}{630000}=1$

$y=700$

The second explosion should be set up at a distance of 700 feet due north of point $\text{B}$.