Chapter 10.2, Problem 75AYU

Gateway Arch The Gateway Arch in St. Louis is often mistaken to be parabolic in shape. In fact, it is a catenary, which has a more complicated formula than a parabola. The Arch is 630 feet high and 630 feet wide at its base.

To determine

To find:

a. The equation of a parabola with the given dimensions. Let $x$ equal the horizontal distance from the center of the arch.

b. With the given height of arch at various widths; find the corresponding heights for the parabola found in (a).

c. Whether the data support the notion that the arch is in the shape of a parabola.

Answer to Problem 75AYU

a. $y=-\frac{2x²}{315}+630$

b. $567ft: 119.7ft;478ft: 267.3ft;308ft: 479.4ft$

c. No.

Explanation of Solution

Given:

The Gateway Arch in St. Louis is often mistaken to be parabolic in shape whose arch is 630 feet high and 630 feet wide at its base.

Calculation:

a. Let us imagine an arch along $x\text{-axis}$ and let it raise along $y\text{-axis}$.

Arch is 630 feet high and is 630 feet wide at its base. Then $\left(0,630\right);\left(315,0\right)$ and $\left(-315,0\right)$ lie on the arch.

The equation of parabola would have the form $y=a{x}^2+c$.

Substituting $\left(0,630\right)$ in the above equation we get,

$c=630$

Hence, $y=a{x}^2+630$.

Substituting $\left(315,0\right)$, we get,

$0=315²a+630$

$a=-630/315²$

Thus, the equation of the parabola with the same given dimension is

$y=-\frac{2x²}{315}+630$

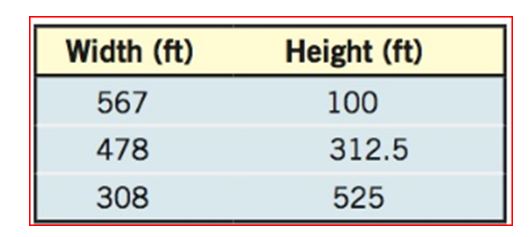
b. To compute the height using the model $y=-\frac{2x²}{315}+630$, we get,

Width	Height	Points	Height using the model
$567$	$100$	$\left(283.5,\text{ h}\right)$	$119.70$
$478$	$312.5$	$\left(239,\text{ h}\right)$	$267.33$
$308$	$525$	$\left(154,\text{ h}\right)$	$479.42$

c. The height computed using the $y=-\frac{2x²}{315}+630$ (from (a)) do not fit the actual heights.

Hence the data does not support the notion that the arch is in the shape of a parabola.