Chapter 10.3, Problem 85AYU

To determine

To find: The shape of an ellipse.

Answer to Problem 85AYU

An ellipse has an eccentricity in the range of $0<e<1$ .

While a circle is the special case $e=0$

Explanation of Solution

Given information:

Eccentricity $=\frac{c}{a},wherea>c$$\tan \theta =a\tan \frac{\theta }{3}$

Calculation:

We know that, the eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.

  

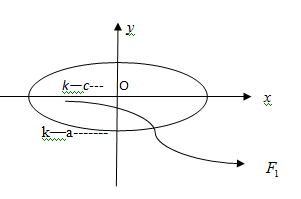
Eccentricity $=\frac{c}{a}$

  $\Rightarrow \boxed{e=\frac{c}{a}}$

When eccentricity closes to $\text{'}0\text{'}$ the shape of the ellipse is circle.

  

Hence, an ellipse has an eccentricity in the range of $0<e<1$ .

While a circle is the special case $e=0$

To determine

To find: The shape of an ellipse.

Answer to Problem 85AYU

Elliptical orbits with increasing eccentricity from $0$ to $1$

Explanation of Solution

Given information:

Eccentricity $=\frac{c}{a},wherea>c$

  $\tan \theta =a\tan \frac{\theta }{3}$

Calculation:

We know that, the eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.

  

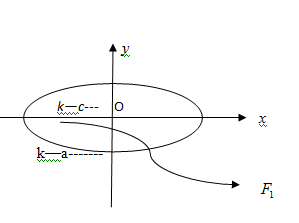
Eccentricity $=\frac{c}{a}$

  $\Rightarrow \boxed{e=\frac{c}{a}}$

Eccentricity $=0.5$

  

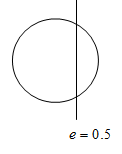
Hence, elliptical orbits with increasing eccentricity from $0$ to $1$

To determine

To find: The shape of an ellipse.

Answer to Problem 85AYU

For a fixed value of the semi-major axis, as the eccentricity, increasing both the semi-minor axis and perihelion distance decreases.

Explanation of Solution

Given information:

Eccentricity $=\frac{c}{a},wherea>c$$\tan \theta =a\tan \frac{\theta }{3}$

Calculation:

We know that, the eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.

  

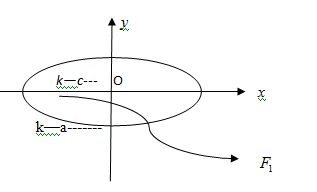
Eccentricity $=\frac{c}{a}$

  $\Rightarrow \boxed{e=\frac{c}{a}}$

Eccentricity close to $1$

  

Hence, for a fixed value of the semi-major axis, as the eccentricity, increasing both the semi-minor axis and perihelion distance decreases.