
Interpretation:
The set of equations (or a small program) to evaluate the constant-volume heat capacity for a moleculeis to be stated. The graph of the result is to be plotted. The trend for the same is to be stated. The heat capacity versus temperature (say from
Concept introduction:
The heat capacity at constant volume for nonlinear polyatomic molecule is given by the formula,
Where,
•
•
•
•
Answer to Problem 18.59E
The set of equations (or a small program) to evaluate the constant-volume heat capacity for a molecule are,
•
•
•
•
•
•
•
The plot between
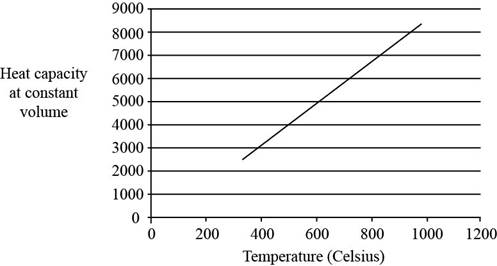
The plot between
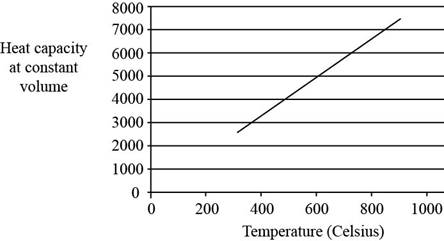
Explanation of Solution
The heat capacity at constant volume for nonlinear polyatomic molecule is given by the formula,
The set of equations(or a small program) to evaluate the constant-volume heat capacity for a molecule are shown below.
•
•
•
•
•
•
•
The vibrational temperatures for
Substitute the value of vibrational temperatures for
The value of
The plot between
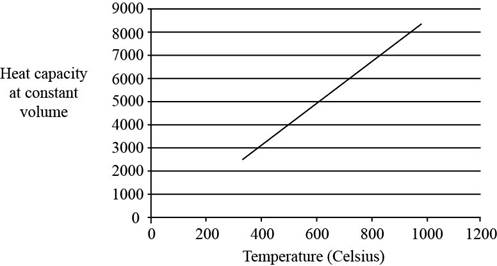
Figure 1
The three vibrational temperatures for
Substitute the value of vibrational temperatures for
The value of
The plot between

Figure 2
The set of equations (or a small program) to evaluate the constant-volume heat capacity for a molecule are,
•
•
•
•
•
•
•
The plot between
Want to see more full solutions like this?
Chapter 18 Solutions
Physical Chemistry
- Draw the major elimination and substitution products formed in this reavtion. Use a dash or wedge bond to indicatr the stereochemistry of substituents on assymetric centers, wheere applicable. Ignore any inorganic byproducts.arrow_forwardDraw the two possible products produced in this E2 elimination. Ignore any inorganic byproductsarrow_forwardDraw the major products of this SN1 reaction. Ignore any inorganic byproducts.arrow_forward
- Draw the major elimination and substitution products formed in this reaction. Use a dash or wedge bond to indicate the stereochemistry of substituents on asymmetric centers, wehre applicable. Ignore and inorganic byproducts.arrow_forwardCurved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electron-pushing arrows for the following reaction or mechanistic step(s). Be sure to account for all bond-breaking and bond-making steps. Drawing Arrows THE Problem 33 of 35 N. C:0 Na + Submit Drag To Pan +arrow_forwardDraw the product of the E2 reaction shown below. Include the correct stereochemistry. Ignore and inorganic byproducts.arrow_forward
- Draw the major producrs of this SN1 reaction. Ignore any inorganic byproducts. Use a dash or wedge bond to indicate the sereochemistry of substituents on asymmetric centers where appllicable.arrow_forward5) Oxaloacetic Acid is an important intermediate in the biosynthesis of citric acid. Synthesize oxaloacetic acid using a mixed Claisen Condensation reaction with two different esters and a sodium ethoxide base. Give your answer as a scheme Hint 1: Your final acid product is producing using a decarboxylation reaction. Hint 2: Look up the structure of oxalic acid. HO all OH oxaloacetic acidarrow_forward20. The Brusselator. This hypothetical system was first proposed by a group work- ing in Brussels [see Prigogine and Lefever (1968)] in connection with spatially nonuniform chemical patterns. Because certain steps involve trimolecular reac tions, it is not a model of any real chemical system but rather a prototype that has been studied extensively. The reaction steps are A-X. B+X-Y+D. 2X+ Y-3X, X-E. 305 It is assumed that concentrations of A, B, D, and E are kept artificially con stant so that only X and Y vary with time. (a) Show that if all rate constants are chosen appropriately, the equations de scribing a Brusselator are: dt A-(B+ 1)x + x²y, dy =Bx-x²y. diarrow_forward
- Problem 3. Provide a mechanism for the following transformation: H₂SO A Me. Me Me Me Mearrow_forwardYou are trying to decide if there is a single reagent you can add that will make the following synthesis possible without any other major side products: xi 1. ☑ 2. H₂O хе i Draw the missing reagent X you think will make this synthesis work in the drawing area below. If there is no reagent that will make your desired product in good yield or without complications, just check the box under the drawing area and leave it blank. Click and drag to start drawing a structure. There is no reagent that will make this synthesis work without complications. : ☐ S ☐arrow_forwardPredict the major products of this organic reaction: H OH 1. LiAlH4 2. H₂O ? Note: be sure you use dash and wedge bonds when necessary, for example to distinguish between major products with different stereochemistry. Click and drag to start drawing a structure. G C टेarrow_forward
 Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning, Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning





