
Concept explainers
Interpretation:
The value of
Concept introduction:
The wavefunction contains all the information about the state of the system. The wavefunction is the function of the coordinates of particles and time. The wavefunction
Answer to Problem 12.56E
The values of
The simple potential energy diagram for this system is shown in Figure 1 and Figure 2.
Explanation of Solution
The value of
Where,
•
•
The value of
Where,
•
The value of
The wavefunction
The value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the wavefunction
The value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the wavefunction
The value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the wavefunction
The value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the value of
Substitute the value of
Thus, the wavefunction
The values of potential energy and
| Energy |
|
The plot between the potential energy with
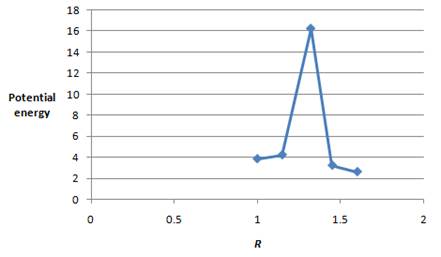
Figure 1
The values of potential energy and
| Energy |
|
The plot between the potential energy with
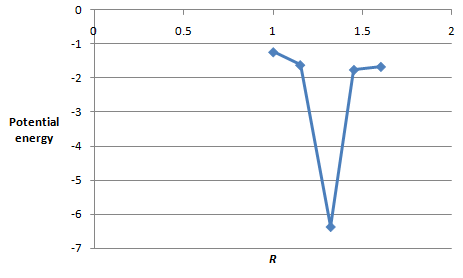
Figure 2
The values of
The simple potential energy diagram for this system is shown in Figure 1 and Figure 2.
Want to see more full solutions like this?
Chapter 12 Solutions
Physical Chemistry
- :0: :0: Select to Add Arrows :0: (CH3)2NH :0: ■ Select to Add Arrows :0: :0: (CH3)2NH ■ Select to Add Arrowsarrow_forwardDraw the product of the following H action sequence. Ignore any inorganic byproducts formed. 1. (CH3CH2)2CuLi, THF 2. CH3Br Q Atoms, Bonds and Rings H Charges ㅁarrow_forwardPlease help me with this the problem is so confusingarrow_forward
- 14 Question (1 point) Disiamylborane adds to a triple bond to give an alkenylborane. Upon oxidation with OH, H2O2, the alkenylborane will form an enol that tautomerizes to an aldehyde. In the first box below, draw the mechanism arrows for the reaction of disiamylborane with the alkyne, and in the last box draw the structure of the aldehyde. 4th attempt Feedback i > 3rd attempt OH, H2O2 i See Periodic Table See Hintarrow_forwardanswer with mechanisms and steps. handwritten please!arrow_forwardHello I need some help with Smartwork. For drawing structure B, I know the correct answer is CH₃B₂, but when I try to type it in, it keeps giving me CH₄BH₃ instead. Do you know how I should write it properly? Should I use a bond or something else?arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
