Chapter 11.10, Problem 30P

A refrigerator operating on the vapor-compression refrigeration cycle using refrigerant-134a as the refrigerant is considered. The temperatures of the cooled space and the ambient air are at 10°F and 80°F, respectively. R-134a enters the compressor at 20 psia as a saturated vapor and leaves at 140 psia and 160°F. The refrigerant leaves the condenser as a saturated liquid. The rate of cooling provided by the system is 45,000 Btu/h. Determine (a) the mass flow rate of R-134a and the COP, (b) the exergy destruction in each component of the cycle and the second-law efficiency of the compressor, and (c) the second-law efficiency of the cycle and the total exergy destruction in the cycle.

To determine

The mass flow rate of R-134a and the COP.

Answer to Problem 30P

The mass flow rate of R-134a and the COP is $\text{0}\text{.2177}\text{lbm}/\text{s}$ and $2.006$ respectively.

Explanation of Solution

Show the T-s diagram for vapor-compression refrigeration cycle as in Figure (1).

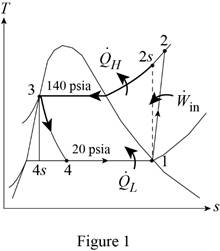
From Figure (1), write the specific enthalpy at state 3 is equal to state 4 due to throttling process.

$h_3\cong h_4$

Here, specific enthalpy at state 3 and 4 is $h_3\text{and}{h}_4$ respectively.

Express the work input.

$w_{\text{in}}=h_2-h_1$ (I)

Here, specific enthalpy at state 2 and 1 is $h_2\text{and}{h}_1$ respectively.

Express heat supplied to the cooled space.

$q_H=h_2-h_3$ (II)

Express the heat removed from the cooled space.

$q_L=q_H-w_{\text{in}}$ (III)

Express quality at state 4.

$h_4=h_{f\text{@20psia}}+x_4{h}_{fg\text{@20psia}}$ (IV)

Here, specific enthalpy at saturated liquid and evaporation and $\text{20}\text{psia}$ is $h_{f\text{@20}\text{psia}}$ and $h_{fg\text{@20}\text{psia}}$ respectively.

Express specific entropy at state 4.

$s_4=s_{f\text{@20}\text{psia}}+x_4{s}_{fg\text{@20}\text{psia}}$ (V)

Here, specific entropy at saturated liquid and evaporation and $\text{20}\text{psia}$ is $s_{f\text{@20}\text{psia}}$ and $s_{fg\text{@20}\text{psia}}$ respectively.

Express mass flow rate of R-134a.

$\dot{m}=\frac{{\dot{Q}}_L}{q_L}$ (VI)

Here, rate of heat lost is ${\dot{Q}}_L$.

Express the COP of the cycle.

$\text{COP}=\frac{q_L}{w_{\text{in}}}$ (VII)

Conclusion:

Refer Table A-12E, “saturated refrigerant-134a-pressure table”, and write the properties corresponding to initial pressure $\left(P_1\right)$ of $\text{20}\text{psia}$.

$\begin{array}{c}{h}_1=h_g\\ =102.71\text{Btu}/\text{lbm}\\ s_1=s_g\\ =0.2257\text{Btu}/\text{lbm}\cdot \text{R}\end{array}$

Here, specific entropy at state 1 is $s_1$, specific enthalpy and entropy at saturated vapor is $h_g\text{and}{s}_g$ respectively.

Refer Table A-13E, “superheated refrigerant-134a”, and write the properties corresponding to pressure at state 2$\left(P_2\right)$ of $\text{140}\text{psia}$ and final temperature $\left(T_2\right)$ of $\text{160°F}$.

$\begin{array}{c}{h}_2=131.37\text{Btu}/\text{lbm}\\ s_2=0.2444\text{Btu}/\text{lbm}\cdot \text{R}\end{array}$

Here, specific entropy at state 2 is $s_2$.

Refer Table A-12E, “saturated refrigerant-134a-pressure table”, and write the properties corresponding to pressure at state 3$\left(P_3\right)$ of $\text{140}\text{psia}$.

$\begin{array}{c}{h}_3=h_f\\ =45.31\text{Btu}/\text{lbm}\\ s_3=s_f\\ =0.09215\text{Btu}/\text{lbm}\cdot \text{R}\end{array}$

Here, specific entropy at state 3 is $s_3$, specific enthalpy and entropy at saturated liquid is $h_f\text{and}{s}_f$ respectively.

As specific enthalpy at state 3 is equal to specific enthalpy at state 4,

$\begin{array}{c}{h}_3\cong h_4\\ =45.31\text{Btu}/\text{lbm}\end{array}$

Refer Table A-12E, “saturated refrigerant-134a-pressure table”, and write the properties corresponding to pressure at state 4$\left(P_4\right)$ of $\text{20}\text{psia}$.

$\begin{array}{c}{h}_{f\text{@20psia}}=11.436\text{Btu}/\text{lbm}\\ h_{fg\text{@20psia}}=91.302\text{Btu}/\text{lbm}\\ s_{f\text{@20}\text{psia}}=0.0260\text{Btu}/\text{lbm}\cdot \text{R}\\ s_{fg\text{@20}\text{psia}}=0.1996\text{Btu}/\text{lbm}\cdot \text{R}\end{array}$

Substitute $45.31\text{Btu}/\text{lbm}$ for $h_4$, $11.436\text{Btu}/\text{lbm}$ for $h_{f\text{@20psia}}$ and $91.302\text{Btu}/\text{lbm}$ for $h_{fg\text{@20psia}}$ in Equation (IV).

$\begin{array}{l}45.31\text{Btu}/\text{lbm}=11.436\text{Btu}/\text{lbm}+\left(x_4\right)91.302\text{Btu}/\text{lbm}\\ x_4=0.3710\end{array}$

Substitute $0.0260\text{Btu}/\text{lbm}\cdot \text{R}\text{and}0.1996\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_{f\text{@20}\text{psia}}$ and $s_{fg\text{@20}\text{psia}}$ respectively and $0.3710$ for $x_4$ in Equation (V).

$\begin{array}{c}{s}_4=\left(0.0260\text{Btu}/\text{lbm}\cdot \text{R}\right)+\left(0.3710\right)\left(0.1996\text{Btu}/\text{lbm}\cdot \text{R}\right)\\ =0.1001\text{Btu}/\text{lbm}\cdot \text{R}\end{array}$

Substitute $\text{131}\text{.37}\text{Btu}/\text{lbm}$ for $h_2$ and $\text{102}\text{.74}\text{Btu}/\text{lbm}$ for $h_1$ in Equation (I).

$\begin{array}{c}{w}_{\text{in}}=\text{131}\text{.37}\text{Btu}/\text{lbm}-\text{102}\text{.74}\text{Btu}/\text{lbm}\\ =28.63\text{Btu}/\text{lbm}\end{array}$

Substitute $\text{131}\text{.37}\text{Btu}/\text{lbm}$ for $h_2$ and $\text{45}\text{.31}\text{Btu}/\text{lbm}$ for $h_3$ in Equation (II).

$\begin{array}{c}{q}_H=\text{131}\text{.37}\text{Btu}/\text{lbm}-\text{45}\text{.31}\text{Btu}/\text{lbm}\\ =86.06\text{Btu}/\text{lbm}\end{array}$

Substitute $86.06\text{Btu}/\text{lbm}$ for $q_H$ and $28.63\text{Btu}/\text{lbm}$ for $w_{\text{in}}$ in Equation (III).

$\begin{array}{c}{q}_L=86.06\text{Btu}/\text{lbm}-28.63\text{Btu}/\text{lbm}\\ =57.43\text{Btu}/\text{lbm}\end{array}$

Substitute $\text{45000}\text{Btu}/\text{h}$ for ${\dot{Q}}_L$ and $57.43\text{Btu}/\text{lbm}$ for $q_L$ in Equation (VI).

$\begin{array}{c}\dot{m}=\frac{\text{45000}\text{Btu}/\text{h}}{57.43\text{Btu}/\text{lbm}}\\ =\frac{\left(\text{45000}\text{Btu}/\text{h}\right)\frac{\text{Btu}/\text{s}}{3600\text{Btu}/\text{h}}}{57.43\text{Btu}/\text{lbm}}\\ =\frac{\text{12}\text{.5}\text{Btu}/\text{s}}{57.43\text{Btu}/\text{lbm}}\\ =0.2177\text{lbm}/\text{s}\end{array}$

Substitute $57.43\text{Btu}/\text{lbm}$ for $q_L$ and $28.63\text{Btu}/\text{lbm}$ for $w_{\text{in}}$ in Equation (VII).

$\begin{array}{c}\text{COP}=\frac{57.43\text{Btu}/\text{lbm}}{28.63\text{Btu}/\text{lbm}}\\ =2.006\end{array}$

Hence, the mass flow rate of R-134a and the COP is $\text{0}\text{.2177}\text{lbm}/\text{s}$ and $2.006$ respectively.

To determine

The exergy destruction in each component of the cycle and the second-law efficiency of the compressor.

Answer to Problem 30P

The exergy destruction in compressor is $\text{2}\text{.203}\text{Btu}/\text{s}$, condenser is $\text{0}\text{.8313}\text{Btu}/\text{s}$, expansion valve is $\text{0}\text{.9358}\text{Btu}/\text{s}$, evaporator is $\text{0}\text{.3996}\text{kJ}/\text{kg}$ and second-law efficiency of the compressor is $\text{64}\text{.7\%}$.

Explanation of Solution

For compressor:

Express the exergy destruction in compressor.

$\begin{array}{c}E{x}_{\text{dest},\text{comp}}=\dot{m}{T}_0{s}_{\text{gen},1-2}\\ =\dot{m}{T}_0\left(s_2-s_1\right)\end{array}$ (VIII)

Here, surrounding temperature is $T_0$, entropy generation during process 1-2 is $s_{\text{gen},1-2}$.

For condenser:

Express the exergy destruction in condenser.

$\begin{array}{c}E{x}_{\text{dest},\text{cond}}=\dot{m}{T}_0{s}_{\text{gen},2-3}\\ =\dot{m}{T}_0\left[\left(s_3-s_2\right)+\frac{q_H}{T_H}\right]\end{array}$ (IX)

Here, entropy generation during process 2-3 is $s_{\text{gen},2-3}$ and high temperature medium is $T_H$.

For expansion valve:

$\begin{array}{c}E{x}_{\text{dest},\exp \text{val}}=\dot{m}{T}_0{s}_{\text{gen},3-4}\\ =\dot{m}{T}_0\left(s_4-s_3\right)\end{array}$ (X)

For evaporator:

Express the exergy destruction in evaporator.

$\begin{array}{c}E{x}_{\text{dest},\text{evap}}=\dot{m}{T}_0{s}_{\text{gen},4-1}\\ =T_0\left[\left(s_1-s_4\right)-\frac{q_L}{T_L}\right]\end{array}$ (XI)

Here, entropy generation during process 4-1 is $s_{\text{gen},4-1}$ and low temperature medium is $T_L$.

Express the power input of the compressor.

${\dot{W}}_{\text{in}}=\dot{m}{w}_{\text{in}}$ (XII)

Express second law efficiency of the compressor.

${\eta }_{\text{II}}=1-\frac{E{x}_{\text{dest},\text{comp}}}{{\dot{W}}_{\text{in}}}\times 100\%$ (XIII)

Conclusion:

Perform unit conversion of surrounding temperature from $\text{°F}\text{to}\text{R}$.

$\begin{array}{c}{T}_0=80\text{°F}\\ =\left(80+460\right)\text{R}\\ =540\text{R}\end{array}$

Perform unit conversion of high temperature medium from $\text{°F}\text{to}\text{R}$.

$\begin{array}{c}{T}_H=80\text{°F}\\ =\left(80+460\right)\text{R}\\ =540\text{R}\end{array}$

Perform unit conversion of low temperature medium from $\text{°F}\text{to}\text{R}$.

$\begin{array}{c}{T}_L=10\text{°F}\\ =\left(10+460\right)\text{R}\\ =470\text{R}\end{array}$

Substitute $\text{0}\text{.2177}\text{lbm}/\text{s}$ for $\dot{m}$, $540\text{R}$ for $T_0$ and $0.2444\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_2$ and $0.2257\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_1$ respectively in Equation (VIII).

$\begin{array}{c}E{x}_{\text{dest},\text{comp}}=\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left(0.2444-0.2257\right)\text{Btu}/\text{lbm}\cdot \text{R}\\ =2.203\text{Btu}/\text{s}\end{array}$

Hence, the exergy destruction in compressor is $2.203\text{Btu}/\text{s}$.

Substitute $\text{0}\text{.2177}\text{lbm}/\text{s}$ for $\dot{m}$, $540\text{R}$ for $T_0$, $\text{86}\text{.06}\text{Btu}/\text{lbm}$ for $q_H$, $\text{540}\text{R}$ for $T_H$, $0.09215\text{Btu}/\text{lbm}\cdot \text{R}\text{and}0.2444\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_3\text{and}{s}_2$ respectively, in Equation (IX).

$\begin{array}{c}E{x}_{\text{dest},\text{cond}}=\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left[\begin{array}{l}\left(0.09215-0.2444\right)\text{Btu}/\text{lbm}\cdot \text{R}\\ +\frac{\text{86}\text{.06}\text{Btu}/\text{lbm}}{\text{540}\text{R}}\end{array}\right]\\ =\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left(0.007073\text{Btu}/\text{lbm}\cdot \text{R}\right)\\ =0.8313\text{Btu}/\text{s}\end{array}$

Hence, the exergy destruction in condenser is $0.8313\text{Btu}/\text{s}$.

Substitute $0.1001\text{Btu}/\text{lbm}\cdot \text{R}\text{and}0.09215\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_4\text{and}{s}_3$ respectively, $\text{0}\text{.2177}\text{lbm}/\text{s}$ for $\dot{m}$, $540\text{R}$ for $T_0$ in Equation (X).

$\begin{array}{c}E{x}_{\text{dest},\exp \text{val}}=\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left(0.1001-0.09215\right)\text{Btu}/\text{lbm}\cdot \text{R}\\ =\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left(0.007961\text{Btu}/\text{lbm}\cdot \text{R}\right)\\ =0.9358\text{Btu}/\text{s}\end{array}$

Hence, the exergy destruction in expansion valve is $0.9358\text{Btu}/\text{s}$.

Substitute $\text{0}\text{.2177}\text{lbm}/\text{s}$ for $\dot{m}$, $540\text{R}$ for $T_0$, $\text{57}\text{.43}\text{Btu}/\text{lbm}$ for $q_L$, $\text{470}\text{R}$ for $T_L$, $0.2257\text{Btu}/\text{lbm}\cdot \text{R}\text{and}0.1001\text{Btu}/\text{lbm}\cdot \text{R}$ for $s_1\text{and}{s}_4$ respectively, in Equation (XI).

$\begin{array}{c}E{x}_{\text{dest},\text{evap}}=\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left[\begin{array}{l}\left(0.2257-0.1001\right)\text{Btu}/\text{lbm}\cdot \text{R}\\ +\frac{57.43\text{Btu}/\text{lbm}}{\text{470}\text{R}}\end{array}\right]\\ =\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(540\text{R}\right)\left(0.003400\text{Btu}/\text{lbm}\cdot \text{R}\right)\\ =0.3996\text{Btu}/\text{s}\end{array}$

Hence, the exergy destruction in evaporator is $0.3996\text{Btu}/\text{s}$.

Substitute $\text{0}\text{.2177}\text{lbm}/\text{s}$ for $\dot{m}$ and $\text{28}\text{.63}\text{Btu}/\text{lbm}$ for $w_{\text{in}}$ in Equation (XII).

$\begin{array}{c}{\dot{W}}_{\text{in}}=\left(\text{0}\text{.2177}\text{lbm}/\text{s}\right)\left(\text{28}\text{.63}\text{Btu}/\text{lbm}\right)\\ =6.232\text{Btu}/\text{s}\end{array}$

Substitute $6.232\text{Btu}/\text{s}$ for ${\dot{W}}_{\text{in}}$ and $2.203\text{Btu}/\text{s}$ for $E{x}_{\text{dest},\text{comp}}$ in Equation (XIII).

$\begin{array}{c}{\eta }_{\text{II}}=1-\frac{2.203\text{Btu}/\text{s}}{6.232\text{Btu}/\text{s}}\times 100\%\\ =0.6465\times 100\%\\ =64.65\%\\ \simeq 64.7\%\end{array}$

Hence, the second-law efficiency of the compressor is $\text{64}\text{.7\%}$.

To determine

The second-law efficiency of the cycle and the total exergy destruction in the cycle.

Answer to Problem 30P

The second-law efficiency of the cycle is $29.9\%$ and the total exergy destruction in the cycle is $\text{4}\text{.370}\text{Btu}/\text{s}$.

Explanation of Solution

Express the exergy of the heat transferred from the low temperature medium.

$\dot{E}{x}_{{\dot{Q}}_L}=-{\dot{Q}}_L\left[1-\frac{T_0}{T_L}\right]$ (XIV)

Determine the second law efficiency of the cycle.

${\eta }_{\text{II}}=\frac{\dot{E}{x}_{{\dot{Q}}_L}}{{\dot{W}}_{\text{in}}}\times 100\%$ (XV)

Express the total exergy destruction in the cycle.

$\dot{E}{x}_{\text{dest,total}}={\dot{W}}_{\text{in}}-\dot{E}{x}_{{\dot{Q}}_L}$ (XVI)

Conclusion:

Substitute $\text{45000}\text{Btu}/\text{h}$ for ${\dot{Q}}_L$, $\text{540}\text{R}\text{and}\text{470}\text{R}$ for $T_0\text{and}{T}_L$ respectively in Equation (XIV).

$\begin{array}{c}\dot{E}{x}_{{\dot{Q}}_L}=-\left(\text{45000}\text{Btu}/\text{h}\right)\left[1-\frac{\text{540}\text{R}}{\text{470}\text{R}}\right]\\ =-\left[\left(\text{45000}\text{Btu}/\text{h}\right)\frac{\text{Btu}/\text{s}}{3600\text{Btu}/\text{h}}\right]\left(-0.1489\right)\\ =-\left(\text{12}\text{.5}\text{Btu}/\text{s}\right)\left(-0.1489\right)\\ =1.862\text{Btu}/\text{s}\end{array}$

Substitute $1.862\text{Btu}/\text{s}$ for $\dot{E}{x}_{{\dot{Q}}_L}$ and $6.232\text{Btu}/\text{s}$ for ${\dot{W}}_{\text{in}}$ in Equation (XV).

$\begin{array}{c}{\eta }_{\text{II}}=\frac{1.862\text{Btu}/\text{s}}{1.862\text{Btu}/\text{s}}\times 100\%\\ =29.9\%\end{array}$

Hence, the second-law efficiency of the cycle is $29.9\%$.

Substitute $1.862\text{Btu}/\text{s}$ for $\dot{E}{x}_{{\dot{Q}}_L}$ and $6.232\text{Btu}/\text{s}$ for ${\dot{W}}_{\text{in}}$ in Equation (XVI).

$\begin{array}{c}\dot{E}{x}_{\text{dest,total}}=6.232\text{Btu}/\text{s}-1.862\text{Btu}/\text{s}\\ =4.370\text{Btu}/\text{s}\end{array}$

Hence, the total exergy destruction in the cycle is $\text{4}\text{.370}\text{Btu}/\text{s}$.