Mechanics of Materials (10th Edition)
10th Edition
ISBN: 9780134319650
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.7, Problem 10.81P
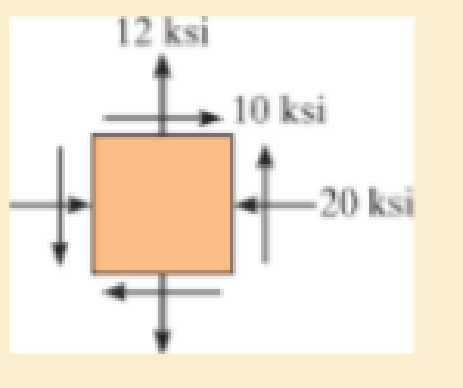
If σY = 50 ksi, determine the factor of safety for this loading against yielding based on (a) the maximum shear stress theory and (b) the maximum distortion energy theory.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A ductile hot-rolled steel bar has a minimum yield strength in tension and compression of 350 MPa. Using the distortion-
energy and maximum-shear-stress theories, determine the factors of safety with the following principal stresses.
σA = 90 MPa, and oß = -98 MPa
The factor of safety from the maximum-shear-stress theory is
"
and the factor of safety from the distortion-energy theory is
If sY = 50 ksi, determine the factor of safety for this loading against yielding based on (a) the maximum shear stress theory and (b) the maximum distortion energy theory.
1. We can visualize the factor of safety for an arbitrary stress using a surface in principal stress space. For
a ductile material that yields according to a von Mises criterion with a yield stress σy, sketch the von
Mises surface in σ₁ - 02 space and sketch the stress surface that corresponds to a factor of safety FoS =
2. For a brittle material that yields according to a max normal (Rankine) criterion with a tensile strength
Gyt and a compressive strength σvc = 20yt, sketch the yield surface and the surface that corresponds
to a factor of safety FoS = 2.
Chapter 10 Solutions
Mechanics of Materials (10th Edition)
Ch. 10.3 - Prove that the sum of the normal strains in...Ch. 10.3 - The state of strain at the point on the arm has...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the leaf of...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain- transformation equations to...
Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain on an...Ch. 10.3 - Determine the equivalent state of strain which...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain, which...Ch. 10.3 - Solve Prob.103 using Mohrs circle. 103. The state...Ch. 10.3 - using Mohrs circle. 103. The state of strain at...Ch. 10.3 - Solve Prob.105 using Mohrs circle. 105. The state...Ch. 10.3 - Solve Prob.108 using Mohrs circle 108. The state...Ch. 10.3 - using Mohrs circle. 106. The state of strain at a...Ch. 10.5 - The strain at point A on the bracket has...Ch. 10.5 - Determine (a) the principal strains at A, (b) the...Ch. 10.5 - Determine (a) the principal strains at A, in the...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained from each...Ch. 10.6 - For the case of plane stress, show that Hookes law...Ch. 10.6 - to develop the strain tranformation equations....Ch. 10.6 - Determine the modulus of elasticity and Polssons...Ch. 10.6 - If it is subjected to an axial load of 15 N such...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - A strain gage having a length of 20 mm Is attached...Ch. 10.6 - Determine the bulk modulus for each of the...Ch. 10.6 - The strain gage is placed on the surface of the...Ch. 10.6 - Determine the associated principal stresses at the...Ch. 10.6 - Determine the applied load P. What is the shear...Ch. 10.6 - If a load of P = 3 kip is applied to the A-36...Ch. 10.6 - The cube of aluminum is subjected to the three...Ch. 10.6 - The principal strains at a point on the aluminum...Ch. 10.6 - A uniform edge load of 500 lb/in. and 350 lb/in....Ch. 10.6 - Prob. 10.45PCh. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - If the material is graphite for which Eg = 800 ksi...Ch. 10.6 - Determine the normal stresses x and y in the plate...Ch. 10.6 - The steel shaft has a radius of 15 mm. Determine...Ch. 10.6 - Prob. 10.51PCh. 10.6 - The A-36 steel pipe is subjected to the axial...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Prob. 10.55PCh. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - Prob. 10.58PCh. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - The yield stress for a zirconium-magnesium alloy...Ch. 10.7 - Solve Prob. 1061 using the maximum distortion...Ch. 10.7 - If a machine part is made of tool L2 steel and a...Ch. 10.7 - Solve Prob.1063 using the maximum distortion...Ch. 10.7 - Prob. 10.65PCh. 10.7 - If a shaft is made of a material for which y = 75...Ch. 10.7 - Solve Prob.1066 using the maximum shear stress...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - The short concrete cylinder having a diameter of...Ch. 10.7 - Prob. 10.70PCh. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - An aluminum alloy is to be used for a solid drive...Ch. 10.7 - If a machine part is made of titanium (TI-6A1-4V)...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - If the 2-in diameter shaft is made from brittle...Ch. 10.7 - If the 2-in diameter shaft is made from cast iron...Ch. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - Prob. 10.82PCh. 10.7 - If the yield stress for steel is Y = 36 ksi,...Ch. 10.7 - Prob. 10.84PCh. 10.7 - The state of stress acting at a critical point on...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - Prob. 10.88PCh. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - The gas tank is made from A-36 steel and has an...Ch. 10.7 - The internal loadings at a critical section along...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10 - In the case of plane stress, where the in-plane...Ch. 10 - The plate is made of material having a modulus of...Ch. 10 - If the material is machine steel having a yield...Ch. 10 - Determine if yielding has occurred on the basis of...Ch. 10 - The 60 strain rosette is mounted on a beam. The...Ch. 10 - Use the strain transformation equations to...Ch. 10 - If the strain gages a and b at points give...Ch. 10 - Use the strain-transformation equations and...Ch. 10 - Use the strain transformation equations to...Ch. 10 - Specify the orientation of the corresponding...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Q1: A ductile bar of aluminum 1010 alloy. Using the distortion-energy and maximum- shear-stress theories determine the factors of safety for the following plane stress states: (α) σχ = 180 MPa, σy = 100 MPa (b) σx = 180 MPa, Txy = (c) σx = -160 MPa, Txy = 150 MPa (d) Txy 100 MPa = 100 MPaarrow_forwardQ1: A ductile bar of aluminum 1010 alloy. Using the distortion-energy and maximum- shear-stress theories determine the factors of safety for the following plane stress states: (a) σx = 180 MPa, σy = 100 MPa (b) σx = 180 MPa, Txy = 100 MPa (c) σx = -160 MPa, Txy = 100 MPa = 150 MPa (d) Txyarrow_forwardDetermine the factor of safety as per tresca's max shear stress theoryarrow_forward
- The state of plane stress at a critical point in a steel machine bracket is shown. If the yield stress for steel is sY = 36 ksi, determine if yielding occurs using the maximum distortion energy theory.arrow_forwardDetermine the yield strength of a material required such that the component would not fail when subject to the following stresses sigma1 = 2 MPa and sigma 2= -15 MPa sigma 3 = 10 MPa). Use a yield criterion that assumes that yield failure will occur when the maximum shear stress in the complex system becomes equal to the limiting shear strength in a simple tensile test.arrow_forwardA loading condition is shown below. The wires at point A and D both made from a steel with the yield strength (Sy) of 190 MPa with 2 mm diameter. Using either maximum shear stress theory or distortion energy theory, determine the maximum load P that can be applied before yielding happens in the wires.arrow_forward
- Determine the diameter of a circular rod made of ductile material with a fatigue strength (complete stress reversal) σe = 280 MPa and a tensile yield strength of 350 MPa. The member is subjected to a varying axial load from 700 kN to – 300 kN. Assume Kt = 1.8 and F.S. = 2.arrow_forwardA brittle material has the properties Sut = 30 kpsi and Suc = 90 kpsi. Using the brittle Coulomb- Mohr and modified- Mohr theories, determine the factors of safety for the following states of plane stress: a. x = 20 kpsi, Txy = −10 kpsi b. σx = - 15 kpsi, σy = 10 kpsi, Txy = -15 kpsiarrow_forwardA thin-walled cylinder of diameter 40 mm is subjected to an internal pressure of 5 N/mm² and a torque of 100 Nm. If the material of the cylinder has a yield stress in simple tension of 150 N/mm determine the required wall thickness using the Tresca and von Mises theories of elastic failure. Ans. 0.81 mm (Tresca), 0.74 mm (von Mises).arrow_forward
- Mechanics Of Material Iarrow_forwardA steel rod of diameter D = 50 mm has a tensile yield strength of 345 MPa supports an axial load P = 50 kN and a vertical load R = 2 kN acting at the end of an 0.8 m long arm. Calculate the strength factor of safety using (a) the maximum normal stress theory, (b) the maximum shear stress theory and (c) the distortion energy theory.arrow_forwardSolve clearly and neatlyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Understanding Failure Theories (Tresca, von Mises etc...); Author: The Efficient Engineer;https://www.youtube.com/watch?v=xkbQnBAOFEg;License: Standard youtube license