Mechanics of Materials (10th Edition)
10th Edition
ISBN: 9780134319650
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.5, Problem 10.27P
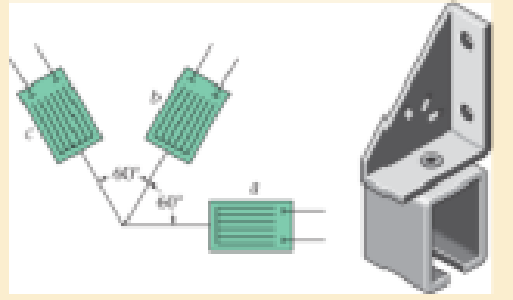
The following readings are obtained for each gage: εa = −780(10−6), εb = 400(10−6), and εc = 500(10−6). Determine (a) the principal strains and (b) the maximum In-plane shear strain and associated average normal strain. In each case show the deformed element due to these strains.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The strain components ɛx, Ey, and yxy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the
principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0p, the
principal strain deformations, and the maximum in-plane shear strain distortion in a sketch.
Ex = 0 HE, ɛy = 380 µɛ, Yxy = 230 µrad. Enter the angle such that -45° s 0,s+45°.
Answer:
Ep1 =
με
Ep2 =
με
Ymax in-plane =
prad
Yabsolute max. =
prad
0, =
The strain components Ex, Ey, and Yxy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the
principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0p, the
principal strain deformations, and the maximum in-plane shear strain distortion in a sketch.
Ex = 0 μE, Ey = 310 με, Yxy = 280 μrad. Enter the angle such that -45° ≤ 0,≤ +45°
Answer:
Ep1 =
Ep2 =
Ymax in-plane =
Yabsolute max. =
0p
=
με
με
urad
urad
The strain components ɛx, ɛy, and Yxy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the
principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0p, the
principal strain deformations, and the maximum in-plane shear strain distortion in a sketch.
Ex = 0 µɛ, ɛy = 430 µɛ, Yxy = 230 µrad. Enter the angle such that -45° s 0,s+45°.
Answer:
Ep1
με
Ep2 =
Ymax in-plane
prad
Yabsolute max.
prad
%3D
Chapter 10 Solutions
Mechanics of Materials (10th Edition)
Ch. 10.3 - Prove that the sum of the normal strains in...Ch. 10.3 - The state of strain at the point on the arm has...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the leaf of...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain- transformation equations to...
Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain on an...Ch. 10.3 - Determine the equivalent state of strain which...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain, which...Ch. 10.3 - Solve Prob.103 using Mohrs circle. 103. The state...Ch. 10.3 - using Mohrs circle. 103. The state of strain at...Ch. 10.3 - Solve Prob.105 using Mohrs circle. 105. The state...Ch. 10.3 - Solve Prob.108 using Mohrs circle 108. The state...Ch. 10.3 - using Mohrs circle. 106. The state of strain at a...Ch. 10.5 - The strain at point A on the bracket has...Ch. 10.5 - Determine (a) the principal strains at A, (b) the...Ch. 10.5 - Determine (a) the principal strains at A, in the...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained from each...Ch. 10.6 - For the case of plane stress, show that Hookes law...Ch. 10.6 - to develop the strain tranformation equations....Ch. 10.6 - Determine the modulus of elasticity and Polssons...Ch. 10.6 - If it is subjected to an axial load of 15 N such...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - A strain gage having a length of 20 mm Is attached...Ch. 10.6 - Determine the bulk modulus for each of the...Ch. 10.6 - The strain gage is placed on the surface of the...Ch. 10.6 - Determine the associated principal stresses at the...Ch. 10.6 - Determine the applied load P. What is the shear...Ch. 10.6 - If a load of P = 3 kip is applied to the A-36...Ch. 10.6 - The cube of aluminum is subjected to the three...Ch. 10.6 - The principal strains at a point on the aluminum...Ch. 10.6 - A uniform edge load of 500 lb/in. and 350 lb/in....Ch. 10.6 - Prob. 10.45PCh. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - If the material is graphite for which Eg = 800 ksi...Ch. 10.6 - Determine the normal stresses x and y in the plate...Ch. 10.6 - The steel shaft has a radius of 15 mm. Determine...Ch. 10.6 - Prob. 10.51PCh. 10.6 - The A-36 steel pipe is subjected to the axial...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Prob. 10.55PCh. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - Prob. 10.58PCh. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - The yield stress for a zirconium-magnesium alloy...Ch. 10.7 - Solve Prob. 1061 using the maximum distortion...Ch. 10.7 - If a machine part is made of tool L2 steel and a...Ch. 10.7 - Solve Prob.1063 using the maximum distortion...Ch. 10.7 - Prob. 10.65PCh. 10.7 - If a shaft is made of a material for which y = 75...Ch. 10.7 - Solve Prob.1066 using the maximum shear stress...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - The short concrete cylinder having a diameter of...Ch. 10.7 - Prob. 10.70PCh. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - An aluminum alloy is to be used for a solid drive...Ch. 10.7 - If a machine part is made of titanium (TI-6A1-4V)...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - If the 2-in diameter shaft is made from brittle...Ch. 10.7 - If the 2-in diameter shaft is made from cast iron...Ch. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - Prob. 10.82PCh. 10.7 - If the yield stress for steel is Y = 36 ksi,...Ch. 10.7 - Prob. 10.84PCh. 10.7 - The state of stress acting at a critical point on...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - Prob. 10.88PCh. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - The gas tank is made from A-36 steel and has an...Ch. 10.7 - The internal loadings at a critical section along...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10 - In the case of plane stress, where the in-plane...Ch. 10 - The plate is made of material having a modulus of...Ch. 10 - If the material is machine steel having a yield...Ch. 10 - Determine if yielding has occurred on the basis of...Ch. 10 - The 60 strain rosette is mounted on a beam. The...Ch. 10 - Use the strain transformation equations to...Ch. 10 - If the strain gages a and b at points give...Ch. 10 - Use the strain-transformation equations and...Ch. 10 - Use the strain transformation equations to...Ch. 10 - Specify the orientation of the corresponding...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The strain components ɛx, ɛy, and yxy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0p, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex = 0 µɛ, ɛy = 380 µɛ, Yxy = 250 prad. Enter the angle such that -45° < 0,s +45. Answer: Ep1 = με Ep2 = με Ymax in-plane prad Yabsolute max. prad %3D 0p =arrow_forwardThe strain components ɛ Ey, and ywyare given for a point in a body subjected to plane strain. Using Mohr's circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex = 0 µE, Ɛy = 330 µɛ, Yxy = 270 prad. Enter the angle such that -45° <0,s+45°. Answer: Ep1 = Ep2 = Ymax in-plane prad Yabsolute max. pradarrow_forwardThe strain components e x, e y, and γ xy are given for a point in a body subjected to plane strain. Using Mohr’s circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle θ p, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex Ey Yxy −1,570 με -430με -950 μradarrow_forward
- The strain components at a point in a body subjected to plane strain are & 850μ, Ey -300μ, and Yay 400μ. Determine the principal strains and the maximum shearing strain at the point. Show the principal strain deformations and the maximum shearing strain distortion on a sketch. = = =arrow_forwardThe strain components ɛ, Ey, and yy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex = 300 µe, ɛ, = -710 pe, Vxy = -440 urad. Enter the angle such that -45°s0,s +45°. Answer: Ep1= pe Ep2= με Ymax in-plane = prad Yabsolute max. prad Əp =arrow_forwardThe strain components εx, εy, and γxy are given for a point in a body subjected to plane strain. Using Mohr’s circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle θp, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. εx = 350 με, εy = -540 με, γxy = -890 μrad. Enter the angle such that -45°≤θp≤ +45°.arrow_forward
- The strain components, ex= 940 micro strain, ey= -360 micro strain and yxy=830micro strain are given for a point in body subjected to plane strain. Determine; a. Magnitude of the principal strains b. The direction of the principal strain axes c. The maximum in-plane shear strain. Confirm your answer by means of Mohr's circle of strain and determine the linear strain on an axis inclined at 20 degrees clockwise to the direction of eyarrow_forwardA strain gauge that is attached to the surface of a stressed componentgives 3 readings (εa = 310, εb = B=150, εc = C=-300). If the strain gauge is of the 60 degreestype (indicating the angle between each of the gauges), construct a Mohr’s StrainCircle. Gauge A is aligned along the x-axis. Using Mohr’s Strain Circle calculate the:(i) principal strains (ε1, ε2) (ii) principal angles (φ1, φ2) (You should measure these anticlockwise from the y-axis)(iii) maximum shear strain in the plane (γmax)arrow_forwardThe state of plane strain on an element is represented by the following components: Ex =D340 x 10-6, ɛ, = , yxy Ey =D110 x 10-6, 3D180 x10-6 ху Draw Mohr's circle to represent this state of strain. Use Mohrs circle to obtain the principal strains and principal plane.arrow_forward
- The strain components E, Ey, and yyare given for a point in a body subjected to plane strain. Using Mohr's circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0p, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex = 440 µE, ɛ, = -810 µE, Vxy = -540 µrad. Enter the angle such that -45°s0,s +45°. Answer: Ep1 = Ep2 = Ymax in-plane prad Yabsolute max. prad 0, =arrow_forwardQ4 A three strain gages have been attached directly to a piston used to raise a medical chair, the strain gages give strains as ɛa = 80 µ , Ep = 60 µ and Ec = 20 µ . Determine the principal strains and the principal strain directions for the given set of strains. And Compute the strain in a direction -30° (clockwise) with the x axis. a,x A c.y Pumparrow_forwardThe strain components εx, εy, and γxy are given for a point in a body subjected to plane strain. Using Mohr’s circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle θp, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch.εx = 0 με, εy = 310 με, γxy = 280 μrad. Enter the angle such that -45° ≤ θp ≤ +45°.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Lec21, Part 5, Strain transformation; Author: Mechanics of Materials (Libre);https://www.youtube.com/watch?v=sgJvz5j_ubM;License: Standard Youtube License