Mechanics of Materials (10th Edition)
10th Edition
ISBN: 9780134319650
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.6, Problem 10.49P
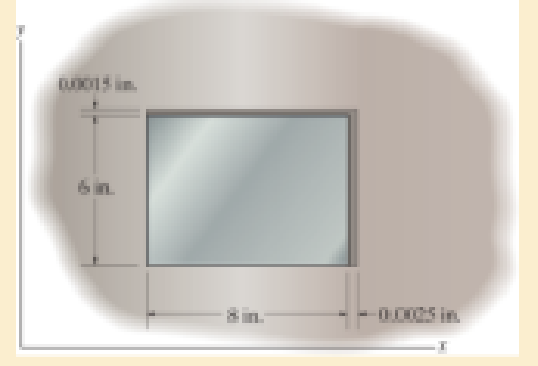
Determine the normal stresses σx and σy in the plate if the temperature is increased by ΔT = 100 °F. Hint: To solve, add the thermal strain αΔT to the equations for Hooke’s law.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Extensometers attached to the external surface of a pressure vessel indicate
that a = 0.002 and & = 0.005 along the longitudinal and transverse directions,
respectively. Determine the corresponding stresses for E= 210 GPa and v =
0.4. What would be the error in these stresses if Poisson's ratio were not
considered?
Solve it correctly.
2. ! SHOW FULL SOLUTION !
* use THERMAL STRESS AND STRAIN FORMULAS
*use DATA GIVEN BELOW
Chapter 10 Solutions
Mechanics of Materials (10th Edition)
Ch. 10.3 - Prove that the sum of the normal strains in...Ch. 10.3 - The state of strain at the point on the arm has...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the pin leaf...Ch. 10.3 - The state of strain at the point on the leaf of...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations and...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Use the strain- transformation equations to...
Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain on an...Ch. 10.3 - Determine the equivalent state of strain which...Ch. 10.3 - Use the strain transformation equations to...Ch. 10.3 - Determine the equivalent state of strain, which...Ch. 10.3 - Solve Prob.103 using Mohrs circle. 103. The state...Ch. 10.3 - using Mohrs circle. 103. The state of strain at...Ch. 10.3 - Solve Prob.105 using Mohrs circle. 105. The state...Ch. 10.3 - Solve Prob.108 using Mohrs circle 108. The state...Ch. 10.3 - using Mohrs circle. 106. The state of strain at a...Ch. 10.5 - The strain at point A on the bracket has...Ch. 10.5 - Determine (a) the principal strains at A, (b) the...Ch. 10.5 - Determine (a) the principal strains at A, in the...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained for each gage:...Ch. 10.5 - The following readings are obtained from each...Ch. 10.6 - For the case of plane stress, show that Hookes law...Ch. 10.6 - to develop the strain tranformation equations....Ch. 10.6 - Determine the modulus of elasticity and Polssons...Ch. 10.6 - If it is subjected to an axial load of 15 N such...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - If it has the original dimensions shown, determine...Ch. 10.6 - A strain gage having a length of 20 mm Is attached...Ch. 10.6 - Determine the bulk modulus for each of the...Ch. 10.6 - The strain gage is placed on the surface of the...Ch. 10.6 - Determine the associated principal stresses at the...Ch. 10.6 - Determine the applied load P. What is the shear...Ch. 10.6 - If a load of P = 3 kip is applied to the A-36...Ch. 10.6 - The cube of aluminum is subjected to the three...Ch. 10.6 - The principal strains at a point on the aluminum...Ch. 10.6 - A uniform edge load of 500 lb/in. and 350 lb/in....Ch. 10.6 - Prob. 10.45PCh. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - A single strain gage, placed in the vertical plane...Ch. 10.6 - If the material is graphite for which Eg = 800 ksi...Ch. 10.6 - Determine the normal stresses x and y in the plate...Ch. 10.6 - The steel shaft has a radius of 15 mm. Determine...Ch. 10.6 - Prob. 10.51PCh. 10.6 - The A-36 steel pipe is subjected to the axial...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Air is pumped into the steel thin-walled pressure...Ch. 10.6 - Prob. 10.55PCh. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - The thin-walled cylindrical pressure vessel of...Ch. 10.6 - Prob. 10.58PCh. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - A material is subjected to plane stress. Express...Ch. 10.7 - The yield stress for a zirconium-magnesium alloy...Ch. 10.7 - Solve Prob. 1061 using the maximum distortion...Ch. 10.7 - If a machine part is made of tool L2 steel and a...Ch. 10.7 - Solve Prob.1063 using the maximum distortion...Ch. 10.7 - Prob. 10.65PCh. 10.7 - If a shaft is made of a material for which y = 75...Ch. 10.7 - Solve Prob.1066 using the maximum shear stress...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - The short concrete cylinder having a diameter of...Ch. 10.7 - Prob. 10.70PCh. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - The plate is made of Tobin bronze, which yields at...Ch. 10.7 - An aluminum alloy is to be used for a solid drive...Ch. 10.7 - If a machine part is made of titanium (TI-6A1-4V)...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The components of plane stress at a critical point...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - The 304-stainless-steel cylinder has an inner...Ch. 10.7 - If the 2-in diameter shaft is made from brittle...Ch. 10.7 - If the 2-in diameter shaft is made from cast iron...Ch. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - Prob. 10.82PCh. 10.7 - If the yield stress for steel is Y = 36 ksi,...Ch. 10.7 - Prob. 10.84PCh. 10.7 - The state of stress acting at a critical point on...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - The shaft consists of a solid segment AB and a...Ch. 10.7 - Prob. 10.88PCh. 10.7 - If Y = 50 ksi, determine the factor of safety for...Ch. 10.7 - The gas tank is made from A-36 steel and has an...Ch. 10.7 - The internal loadings at a critical section along...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10.7 - If the material is machine steel having a yield...Ch. 10 - In the case of plane stress, where the in-plane...Ch. 10 - The plate is made of material having a modulus of...Ch. 10 - If the material is machine steel having a yield...Ch. 10 - Determine if yielding has occurred on the basis of...Ch. 10 - The 60 strain rosette is mounted on a beam. The...Ch. 10 - Use the strain transformation equations to...Ch. 10 - If the strain gages a and b at points give...Ch. 10 - Use the strain-transformation equations and...Ch. 10 - Use the strain transformation equations to...Ch. 10 - Specify the orientation of the corresponding...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What is an uninitialized variable?
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
What are the design issues for character string types?
Concepts Of Programming Languages
17–1C A high-speed aircraft is cruising in still air. How does the temperature of air at the nose of the aircra...
Thermodynamics: An Engineering Approach
Assume a telephone signal travels through a cable at two-thirds the speed of light. How long does it take the s...
Electric Circuits. (11th Edition)
Why is the study of database technology important?
Database Concepts (8th Edition)
Computers process data under the control of sets of instructions called
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- At a point on the free surface of a ductile cast iron [E = 168 GPa; ν = 0.32; α = 10.8×10– 6 /°C] machine part, the measured strains resulting from both a temperature decrease of 65°C and externally applied loads are εx = −370 με, εy = −715 με, and γ xy = 0. Determine the stresses σ x and σ y at the point.arrow_forward* Your answer is incorrect. A spherical rubber balloon is blown up until its diameter is three times the initial diameter. If E = 10750 psi and v=0.46, determine the stresses in the balloon. Assume the stress-strain behavior is linear. Answer: 0 = 268.75 ksiarrow_forwardThe material is subjected to biaxial loading producing uniform normal stress x and y as shown. The strains are Strainx=−0.00065 and Strainy=−0.00040. Use E=30×106 psi and v=0.30. Determine the following: (a) stress at x. Indicate tension or compression. Use 2 decimal places. (b) stress at y. Indicate tension or compression. Use 2 decimal places. (c) Change in the thickness of the material. Indicate elongation or contraction. Use 5 decimal places and scientific notation of ×10−3(Example: _ . _ _ _ _ _ ×10−3)arrow_forward
- A plane stress state is given by the principal stresses σx =25 MPa and σy= -11 MPa. Determine σx' in the case that the system is inclined by 30 degrees (counter-clockwise). Give your answer in MPa to the nearest whole number.arrow_forwardElectrical strain gauges were applied to a notched specimen, the results were εx = 0.19 and Ey = -0.068. If the material is aluminum (E = 71700 MPa and v = 0.333), find σy in MPa to determine the stresses in the notch. Use Excel spreadsheet posted on Canvas and give correct answer to one decimal place. Εγ Y Exarrow_forward3. The aluminum and bronze cylinders are centered and secured between two rigid end-plates by tightening the two steel bolts. There is no axial load in the assembly at a temperature of 50 °F. Find the stress in the steel bolts when the temperature is increased to 200 °F. Use the following data: 1.0 in. -3 in.→-4 in.- A (in?) a (l°F) E (psi) -1.0 in. Aluminum cylinder Bronze cylinder 1.75 12.8 x 10° 10 x 106 2.50 10.5 x 10° 12 x 10° Each steel bolt 0.75 6.5 x 10° 29 x 10° Aluminum Bronzearrow_forward
- A steel rod, 5m in length, is 100 sq. mm at the cross-section. The rod is in its original length at 20 degrees Celsius. Determine the thermal strain at 70 degrees Celsius if the rod is unrestricted? Use α= 11.7 x 10^-6 per degree Celsiusarrow_forwardA carbon steel ball with 27-mm diameter is pressed together with an aluminum ball with a 35-mm diameter by a force of 11 N. Determine the maximum shear stress and the depth at which it will occur for the aluminum ball. Assume the figure given below, which is based on a typical Poisson's ratio of 0.3, is applicable to estimate the depth at which the maximum shear stress occurs for these materials. Ratio of stress to Pma σ. T 1.0 0.8 0.6 0.4 0.2 0 J₂, J₂ 0.5a σ₂ Tmax a 2a Distance from contact surface 1.5a 2.5a 3a The maximum shear stress is determined to be 134.6 Z MPa. The depth in the aluminum ball at which the maximum shear stress will occur is determined to be 0.0519 mm.arrow_forwardAt a point in the cross-section of an engineering component an element is subject to the following stresses: σx =100MPa σy =45MPa τxy = -50MPa Construct a Mohr’s Stress Circle and hence determine: (a) The Principal Stresses (σ1 & σ2) and the Directions of the Principal Planes (φ1 & φ2) (b) The Maximum Shear Stress (τmax) (c) Find the Normal Stress (σn) acting on a plane at 40 degs anticlockwise from the y-axisarrow_forward
- A single strain gage forming an angle = 18° with a horizontal plane is used to determine the gage pressure in the cylindrical steel tank shown. The cylindrical wall of the tank is 6 mm thick, has a 600-mm inside diameter, and is made of a steel with E= 200 GPa and v = 0.30. Determine the pressure in the tank indicated by a strain gage reading of 320μ. (Round the final answer to three decimal places.) The pressure in the tank is MPa.arrow_forwardThe rigid bar ABCD of negligible weight is initially horizontal, and the steel rods attached at A and C are stress free. 26 kips load is then applied and the temperature of the steel rods is changed by AT. Find AT for which the stresses in two steel rods will be equal. Use a = 6.5 x 10"/°F and E = 29 x 10°psi for steel. A = 0.6 sq. in 3 ft 5 ft 5 ft D A 3 ft B 4 ft A = 0.8 sq. in V 26 kipsarrow_forwardA 60 ̊ strain rosette measures the following strain at a point on the aluminum skin of an airplane. ε0 = 160 ×10-6 m/m, ε60 = -220 ×10-6 m/m and ε120 = 360 ×10-6 m/m. Using E= 10 ×106 psi and v = 0.3, Determine the principle stresses and the maximum in-plane shear stress.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Lec21, Part 5, Strain transformation; Author: Mechanics of Materials (Libre);https://www.youtube.com/watch?v=sgJvz5j_ubM;License: Standard Youtube License