Chapter 6.5, Problem 4E

(a)

To determine

Approximate the value of integral using Trapezoidal rule with $n=4$ .

Answer to Problem 4E

With $n=4$ :

  ${\displaystyle {\int }_1^2\frac{1}{x}dx}\approx 0.697$

Explanation of Solution

Given information:

  ${\displaystyle {\int }_1^2\frac{1}{x}dx}$

Since we are required to use the Trapezoidal rule, first we need to find the height.

  $h=\frac{b-a}{n}=\frac{2-1}{4}=\frac{1}{4}$

Function values:

  

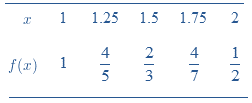
Now,

Setup the equation:

  ${\displaystyle {\int }_1^2\frac{1}{x}dx}\approx \frac{1/4}{2}\left[f\left(1\right)+2\cdot f\left(1.25\right)+2\cdot f\left(1.5\right)+2\cdot f\left(1.75\right)+f\left(2\right)\right]$

Plugin the values into the equation:

  $\begin{array}{l}{\displaystyle {\int }_1^2\frac{1}{x}dx}=\frac{1}{8}\left[1+2\cdot \left(\frac{4}{5}\right)+2\cdot \left(\frac{2}{3}\right)+2\cdot \left(\frac{4}{7}\right)+\frac{1}{2}\right]\\ =\frac{1}{8}\left[1+\frac{8}{5}+\frac{4}{3}+\frac{8}{7}+\frac{1}{2}\right]\\ =\frac{1171}{1680}\\ \approx 0.697\end{array}$

(b)

To determine

Whether the approximation is an overestimate or an under − estimate.

Answer to Problem 4E

The approximation is an overestimate.

Explanation of Solution

Given information:

  ${\displaystyle {\int }_1^2\frac{1}{x}dx}$

First derivative of the function:

  $f\text{'}\left(x\right)=-x^{-2}$

Second derivative of the function:

  $f\text{'}\text{'}\left(x\right)=\frac{2}{x^3}$

We know that

Second derivative gives the concavity.

If the second derivative is greater than 0,

It’s an overestimate.

If the second derivative is less than 0,

It’s an underestimate.

Note that

The value of second derivative is $\frac{2}{x^3}$ which is greater than 0.

Therefore,

The approximation is an overestimate.

(c)

To determine

Integral’s exact value to verify the answer.

Answer to Problem 4E

The exact value of integral is approx. 0.6931 which is not same as using the Trapezoidal rule with $n=4$ .

Explanation of Solution

Given information:

  ${\displaystyle {\int }_1^2\frac{1}{x}dx}$

Using FTC (Fundamental Theorem of Calculus):

  $\begin{array}{l}{\displaystyle {\int }_1^2\frac{1}{x}dx}={\ln \left|x\right||}_1^2\\ =\ln 2-\ln 1\\ =\ln 2-0\\ =\ln 2\\ \approx 0.6931\end{array}$

Therefore,

Integral’s exact value is approx. 0.6931 which is not same as the value of integral obtained in Part (a).