Chapter 6, Problem 34RE

(a)

To determine

To calculate:The upper estimate and lower estimate for the distance travelled by the shed.

Answer to Problem 34RE

The lower estimate is 87.15 ft and the upper estimate is 103.05 ft

Explanation of Solution

Given information:

A speedometer in the sled monitors its speed, which is recorded at 3-second intervals during the 27-second run.

  

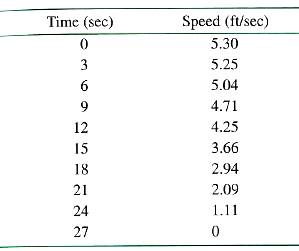
Formula used:

The upper estimate and lower estimate method is used.

Calculation:

(a) For upper estimate, sum the speeds from zero second to 24 second and then multiplied by 3, the speeds from 0 second for calculating the upper estimate because values of speed are decreasing. Hence, it is decreasing function and to get an upper estimate in decreasing function, to apply left-hand pint rectangular approximation method.

  $\begin{array}{l}\left(\begin{array}{l}\text{upper estimate}\\ \text{for distance}\\ \text{traveled}\end{array}\right)=3\left(\begin{array}{l}5.30+5.25+5.04+4.71+4.25+\\ 3.66+2.94+2.09+1.11\end{array}\right)\\ =3\times 34.35\\ \left(\begin{array}{l}\text{upper estimate}\\ \text{for distance}\\ \text{traveled}\end{array}\right)=103.05\text{ft}\end{array}$

For lower estimate, sum the speeds from three second to 27 second and then multiplied by 3, the speeds from 3 second for calculating the lower estimate because values of speed are decreasing. Hence, it is decreasing function and to get a lower estimate in decreasing function, to apply right-hand pint rectangular approximation method.

  $\begin{array}{l}\left(\begin{array}{l}\text{lower estimate}\\ \text{for distance}\\ \text{traveled}\end{array}\right)=3\left(\begin{array}{l}5.25+5.04+4.71+4.71+4.25+\\ 3.66+2.94+2.09+1.11+0\end{array}\right)\\ =3\times 29.05\\ \left(\begin{array}{l}\text{lower estimate}\\ \text{for distance}\\ \text{traveled}\end{array}\right)=87.15\text{ft}\end{array}$

Conclusion:

The lower estimate is 87.15 ft and the upper estimate is 103.05 ft

(b)

To determine

To find:the distance travelled by the sled.

Answer to Problem 34RE

The value of the integral is ${\displaystyle \underset{0}{\overset{27}{\int }}f\left(x\right)}dx=95.1\text{ft}$

Explanation of Solution

Formula used:

  $h=\frac{b-a}{n}$

Calculation:

In the trapezoidal rule, if [ a, b ] is partitioned into n subintervals of equal length $h=\frac{b-a}{n}$ , the graph of f on [ a, b ] can be approximated by a straight line segment at each subinterval. The region between the curve and the x-axis is then approximated by the trapezoids, the area of each trapezoid being the length of its horizontal “altitude" times the average of two vertical “bases".

That is,

  $\begin{array}{l}{\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)}dx=h\frac{y_0+y_1}{2}+h\frac{y_1+y_2}{2}+\mathrm{.....}+h\frac{y_{n-1}+y_n}{2}\\ =h\left(\frac{y_0}{2}+y_1+y_2+\mathrm{....}+y_{n-1}+\frac{y_n}{2}\right)\\ {\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)}dx=\frac{h}{2}\left(y_0+2y_1+2y_2+\mathrm{.....}+2y_{n-1}+y_n\right)\end{array}$

Where,

  $\begin{array}{l}{y}_0=f\left(a\right)\\ y_1=f\left(x_1\right)\\ .\\ .\\ y_{n-1}=f\left(x_{n-1}\right)\\ y_n=f\left(b\right)\end{array}$

Now, apply the trapezoidal rule with

  $\begin{array}{l}n=9\\ \left[a,b\right]=\left[0,27\right]\end{array}$

So,

  $\begin{array}{l}h=\frac{b-a}{n}\\ =\frac{27-0}{9}\\ h=3\end{array}$

The given table is shown below,

  

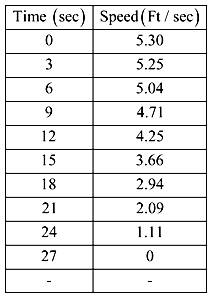
To apply the trapezoidal rule,

To take ‘time’ as $x_0=0$ and the corresponding speed as $y_0=5.30$

Similarly by taking the remaining tabular values as shown in the following table,

  

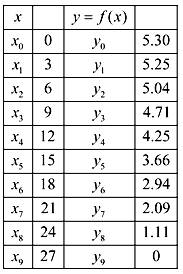
Now, substitute the values from given table in this equation

  $\begin{array}{l}{\displaystyle \underset{0}{\overset{27}{\int }}f\left(x\right)}dx=\text{distance}\text{traveled}\\ =\frac{h}{2}\left(y_0+2y_1+2y_2+2y_3+2y_4+2y_5+2y_6+2y_7+2y_8+y_9\right)\\ =\frac{3}{2}\left(\begin{array}{l}5.30+2\left(5.25\right)+2\left(5.04\right)+2\left(4.71\right)+2\left(4.25\right)\\ +2\left(3.66\right)+2\left(2.94\right)+2\left(2.09\right)+2\left(1.11\right)+0\end{array}\right)\\ {\displaystyle \underset{0}{\overset{27}{\int }}f\left(x\right)}dx=95.1\text{ft}\end{array}$

Conclusion:

The value of the integral is ${\displaystyle \underset{0}{\overset{27}{\int }}f\left(x\right)}dx=95.1\text{ft}$