Chapter 6.5, Problem 38E

(a)

To determine

To find: To calculate the value of $f^{\left(4\right)}\left(x\right)$ .

Answer to Problem 38E

  $f^{\left(4\right)}\left(x\right)=-48x^2\cos \left(x^2\right)+\sin \left(x^2\right)\left(16x^4-12\right)$

Explanation of Solution

Given information:

  $f\left(x\right)=\sin \left(x^2\right)$

Formula Used:

Product rule of differentiation:

  $\frac{d}{dx}\left[f\left(x\right)g\left(x\right)\right]=f\left(x\right)g\text{'}\left(x\right)+g\left(x\right)f\text{'}\left(x\right)$

Calculation:

  $f\left(x\right)=\sin \left(x^2\right)$

  $f\text{'}\left(x\right)=2x\cos \left(x^2\right)$

  $f\text{'}\text{'}\left(x\right)=2\left[x\left(-2x\sin \left(x^2\right)\right)+\cos \left(x^2\right)\right]$

  $=-4x^2\sin \left(x^2\right)+2\cos \left(x^2\right)$

  $=2\left[\cos \left(x^2\right)-2x^2\sin \left(x^2\right)\right]$

  $f^{\left(3\right)}\left(x\right)=2\left[-2x\sin \left(x^2\right)-2\left[2x^3\cos \left(x^2\right)+2x\sin \left(x^2\right)\right]\right]$

  $=4\left[-x\sin \left(x^2\right)-2x^3\cos \left(x^2\right)-2x\sin \left(x^2\right)\right]$

  $=4\left[-2x^3\cos \left(x^2\right)-3x\sin \left(x^2\right)\right]$

  $f^{\left(4\right)}\left(x\right)=4\left[4x^4\sin \left(x^2\right)-6x^2\cos \left(x^2\right)-\left[6x^2\cos \left(x^2\right)+3\sin \left(x^2\right)\right]\right]$

  $=4\left[-12x^2\cos \left(x^2\right)+4x^4\sin \left(x^2\right)-3\sin \left(x^2\right)\right]$

  $=-48x^2\cos \left(x^2\right)+\sin \left(x^2\right)\left(16x^4-12\right)$

∴ $f^{\left(4\right)}\left(x\right)=-48x^2\cos \left(x^2\right)+\sin \left(x^2\right)\left(16x^4-12\right)$

(b)

To determine

To graph:To sketch the graph of $y=f^{\left(4\right)}\left(x\right)$ in the viewing window $\left[-1,1\right]$ by $\left[-30,30\right]$

Explanation of Solution

Given information: $y=f^{\left(4\right)}\left(x\right)$

From part (a), $f^{\left(4\right)}\left(x\right)=-48x^2\cos \left(x^2\right)+\sin \left(x^2\right)\left(16x^4-12\right)$

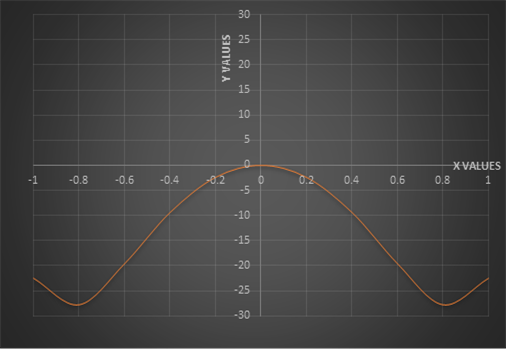
Graph:

The graph of $y=f^{\left(4\right)}\left(x\right)$ where $-1\le x\le 1$ and $-30\le y\le 30$ is shown below

  

(c)

To determine

To explain $\left|f^{\left(4\right)}\left(x\right)\right|\le 30$ for $-1\le x\le 1$

Explanation of Solution

Given Information:The graph of $f^{\left(4\right)}\left(x\right)=-48x^2\cos \left(x^2\right)+\sin \left(x^2\right)\left(16x^4-12\right)$ for $-1\le x\le 1$ as in part (b)

From the above graph it is cleared that $-30\le f^{\left(4\right)}\left(x\right)\le 30$ for all x in $-1\le x\le 1$

∴ $\left|f^{\left(4\right)}\left(x\right)\right|\le 30$ for all x in $-1\le x\le 1$

(d)

To determine

To prove the error estimate for Simpson’s Rule for the above function is $\left|E_S\right|\le \frac{h^4}{3}$ .

Explanation of Solution

Given information:

From part (c) $\left|f^{\left(4\right)}\left(x\right)\right|\le 30$ for all x in $-1\le x\le 1$

Formula Used:

The Error Estimate for Simpson’s Rule:

If $\left|f^{\left(4\right)}\right|$ is continuous and M is any upper bound for the values of $\left|f^{\left(4\right)}\right|$ on $\left[a,b\right]$ , then the error $E_S$ in the Simpson’s Rule approximation of the integral of f from a to b satisfies the inequality:

  $\left|E_S\right|\le \frac{b-a}{180}{h}^{4}M$

Calculation:

Since $\left|f^{\left(4\right)}\left(x\right)\right|\le 30$ for all x in $-1\le x\le 1$

  $a=-1,b=1$ and $M=30$

∴ $\left|E_S\right|\le \frac{1-(-1)}{180}{h}^{4}30$

  $=\frac{2}{180}{h}^{4}30=\frac{h^4}{3}$

∴ $\left|E_S\right|\le \frac{h^4}{3}$

(e)

To determine

To prove the error estimate for Simpson’s Rule will be less than or equal to $0.01$ if $h\le 0.4$

Explanation of Solution

Given information:

From part (d) error estimate for Simpson’s Rule for $y=f^{\left(4\right)}\left(x\right)$ in $\left[-1,1\right]$ is $\left|E_S\right|\le \frac{h^4}{3}$

Calculation:

If $h\le 0.4$

  $\begin{array}{c}\left|E_S\right|\le \frac{h^4}{3}\\ \le \frac{{0.4}^4}{3}=0.008533\prec 0.01\end{array}$

∴Error estimate for Simpson’s Rule is less than or equal to $0.01$

(f)

To determine

To find: To calculate the value of n if $h\le 0.4$ .

Answer to Problem 38E

n must be at least 5 for $h\le 0.4$

Explanation of Solution

Given information:

  $a=-1,b=1$ and $h\le 0.4$

Calculation:

  $\begin{array}{c}h=\frac{b-a}{n}\\ =\frac{1-(-1)}{n}=\frac{2}{n}\end{array}$

If $h\le 0.4$

  $\Rightarrow \frac{2}{n}\le 0.4$

  $\Rightarrow 2\le 0.4\left(n\right)$

  $\Rightarrow \frac{2}{0.4}\le \left(n\right)$

  $\Rightarrow n\ge 5$

∴ n must be at least 5 for $h\le 0.4$