Mechanics of Materials (10th Edition)
10th Edition
ISBN: 9780134319650
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3, Problem 3.9RP
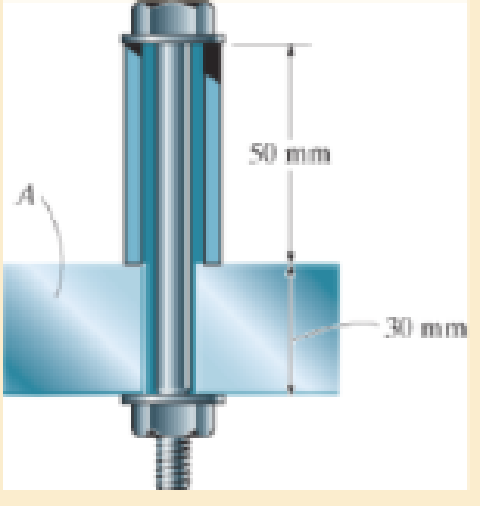
The 8-mm-diameter bolt is made of an aluminum alloy. It fits through a magnesium sleeve that has an inner diameter of 12 mm and an outer diameter of 20 mm. If the original lengths of the bolt and sleeve are 80 mm and 50 mm, respectively, determine the strains in the sleeve and the bolt if the nut on the bolt is tightened so that the tension in the bolt is 8 kN. Assume the material at A is rigid Eal = 70 GPa, Emg = 45 GPa
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Question 1
A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its
ratio of static thrust coefficient to static torque coefficient is 10. The propeller's
integrated lift coefficient is 0.3.
(L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²)
X
A
ΕΙ
B
L
Y
M
Calculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m.
The following choices are provided in units of MPa and rounded to three decimal places.
Select one:
○ 1.2681.818
O 2. 25745.455
O 3. 17163.636
O 4. 10727.273
○ 5.5363.636
Chapter 3 Solutions
Mechanics of Materials (10th Edition)
Ch. 3.4 - Define a homogeneous material.Ch. 3.4 - Indicate the points on the stress-strain diagram...Ch. 3.4 - Define the modulus of elasticity E.Ch. 3.4 - At room temperature, mild steel is a ductile...Ch. 3.4 - Engineering stress and strain are calculated using...Ch. 3.4 - As the temperature increases the modulus of...Ch. 3.4 - A 100-mm-long rod has a diameter of 15 mm. If an...Ch. 3.4 - A bar has a length of 8 in. and cross-sectional...Ch. 3.4 - A 10-mm-diameter rod has a modulus of elasticity...Ch. 3.4 - The material for the 50-mm-long specimen has the...
Ch. 3.4 - The material for the 50-mm-long specimen has the...Ch. 3.4 - If the elongation of wire BC is 0.2 mm after the...Ch. 3.4 - A tension test was performed on a steel specimen...Ch. 3.4 - Data taken from a stress-strain test for a ceramic...Ch. 3.4 - Data taken from a stress-strain test for a ceramic...Ch. 3.4 - The stress-strain diagram for a steel alloy having...Ch. 3.4 - The stress-strain diagram for a steel alloy having...Ch. 3.4 - The stress-strain diagram for a steel alloy having...Ch. 3.4 - The rigid beam is supported by a pin at C and an...Ch. 3.4 - The rigid beam is supported by a pin at C and an...Ch. 3.4 - Acetal plastic has a stress-strain diagram as...Ch. 3.4 - The stress-strain diagram for an aluminum alloy...Ch. 3.4 - The stress-strain diagram for an aluminum alloy...Ch. 3.4 - The stress-strain diagram for an aluminum alloy...Ch. 3.4 - A bar having a length of 5 in. and cross-sectional...Ch. 3.4 - The rigid pipe is supported by a pin at A and an...Ch. 3.4 - The rigid pipe is supported by a pin at A and an...Ch. 3.4 - Direct tension indicators are sometimes used...Ch. 3.4 - The rigid beam is supported by a pin at C and an...Ch. 3.4 - The rigid beam is supported by a pin at C and an...Ch. 3.4 - The stress-strain diagram for a bone is shown, and...Ch. 3.4 - The stress-strain diagram for a bone is shown and...Ch. 3.4 - The two bars are made of a material that has the...Ch. 3.4 - The two bars are made of a material that has the...Ch. 3.4 - The pole is supported by a pin at C and an A-36...Ch. 3.4 - The bar DA is rigid and is originally held in the...Ch. 3.7 - A 100-mm-long rod has a diameter of 15 mm. If an...Ch. 3.7 - A solid circular rod that is 600 mm long and 20 mm...Ch. 3.7 - A 20-mm-wide block is firmly bonded to rigid...Ch. 3.7 - A 20-mm-wide block is bonded to rigid plates at...Ch. 3.7 - The acrylic plastic rod is 200 mm long and 15 mm...Ch. 3.7 - The plug has a diameter of 30 mm and fits within a...Ch. 3.7 - The elastic portion of the stress-strain diagram...Ch. 3.7 - The elastic portion of the stress-strain diagram...Ch. 3.7 - The brake pads for a bicycle tire are made of...Ch. 3.7 - The lap joint is connected together using a 1.25...Ch. 3.7 - The lap joint is connected together using a 1.25...Ch. 3.7 - The rubber block is subjected to an elongation of...Ch. 3.7 - The shear stress-strain diagram for an alloy is...Ch. 3.7 - A shear spring is made from two blocks of rubber,...Ch. 3 - The elastic portion of the tension stress-strain...Ch. 3 - The elastic portion of the tension stress-strain...Ch. 3 - The rigid beam rests in the horizontal position on...Ch. 3 - The wires each have a diameter of 12 in., length...Ch. 3 - The wires each have a diameter of 12 in., length...Ch. 3 - diameter steel bolts. If the clamping force in...Ch. 3 - The stress-strain diagram for polyethylene, which...Ch. 3 - The pipe with two rigid caps attached to its ends...Ch. 3 - The 8-mm-diameter bolt is made of an aluminum...Ch. 3 - An acetal polymer block is fixed to the rigid...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- If L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as (Please select the correct value of σ given in Pa and rounded to three decimal places.) Select one: ○ 1. 1409.193 2. 845.516 O 3. 11273.545 ○ 4.8455.159 ○ 5.4509.418 6. 2818.386 7.5636.772arrow_forwardTo calculate the rotation at Point B, a suitable virtual structure needs to be created. Which equation in the following choices most accurately represents the functional relationship between the bending moment, Mv2 ( Units: N.mm), of the virtual structure and the spatial coordinate x (Units: mm) if the applied unit virtual moment is clockwise? Select one: O 1. Mv2 1.000 O 2. Mv2=x+1.000 O 3. Mv2=x+0.000 4. Mv2 = -x-1.000 O 5. Mv2 -1.000 6. Mv2=-x+0.000arrow_forwardThe vertical deflection at Point B can be calculated as ( The following choices are provided in units of mm and rounded to three decimal places ; the downward deflection is negative and upward deflection is positive. ) Select one: 1. 1703.065 2. -1703.065 3. -2043.679 4.1362.452 5. -1362.452 6. 2043.679arrow_forward
- The second moments of area about z-axis, /z, and the second moments of area about y-axis, ly, can be calculated as Select one: O 1. I = Iz ○ 2. Ly ○ 3. ○ 4. ○ 5. = = Iz = *D' 64 I₁ = D, Iz Ly Ly = 32 *D' = = 3 Iz = *D' 32 = *D' O 6. Iy=D, Ly = D², Iz = 32 O 7. Ly = Iz D = 64 32arrow_forward[If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.] Step -2 Which equation in the following choices most accurately represents the functional relationship between the value of the slope O (Units: Radian) at half length (x = L/2) of the beam and the second moment of area about z-axis, Izz (Units: mm²), of the cross section? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1.0 448787.925/Izz O 2.0 279167.292/Izz O 3.0 38871.395/Izz O 4.0 114847.304/Izz O 5.0 176688.160/Izz O 6.0 609574.150/Izz O 7.0 70675.264/Izzarrow_forwardUse the principle of virtual work to determine the vertical deflection and rotation at tip (Point B) of the cantilever shown below. (L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) q Y M X A ΕΙ B L Step -1 Let the coordinates defined with origin located at B and x-axis pointing to the Left and Y-axis pointing upward. The bending moment, M (Units: N.mm), in the beam as a function of spatial coordinate x(Units: mm) can be most accurately described by Select one: 1. M=1126839.200 +2132.400*x*x 2. M=-1408549.000 - 3198.600*x*x 3. M=-1408549.000-2665.500*x*x 4. M=-1408549.000-2132.400*x*x 5. M= -1408549.000+2665.500*x*x 6. M= 1408549.000 + 2665.500*x*x 7. M= 1408549.000-2665.500*x*xarrow_forward
- Calculate the principal stress σ at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.5363.64 O 2. 12872.727 3.9118.182 4. 10727.273 5. 16090.909 6. 2681.818arrow_forwardQuestion2 The mission profile for a jet driven aircraft consists of the following segments: engine start and warm-up, taxi, take-off, climb to the cruise altitude of 35000 ft, descend to 10000 ft, one hour loiter at this altitude at 60% of the cruise speed, flight at loiter speed and altitude to an alternate airport (100 nm), descend to landing approach condition followed by the final landing, taxi and shutdown. The cruise Mach number is 0.8. No provisions are made for the reserved fuel or any trapped oil and fuel. The aircraft carries 200 people (including pilots and the cabin crew) at 175 lb each and 90 lb baggage each. This aircraft has a wing area of 2000 ft² L/D at cruise L/D at 10000ft flight Table Q2 20 16 0.43 lb/hr/lb 0.50 lb/hr/lb C: Specific Fuel Consumption at cruise: C: Specific Fuel Consumption at 10000 ft flight: Weight ratios Engine Start and warm-up Taxi Take-off Climb Descent Landing, taxi and shutdown 0.992 0.996 0.996 0.996 0.992 0.992 Question 2 continues on the…arrow_forwardCalculate the principal stress σ1_at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: O 1.25745.455 O 2. 32181.818 3. 21454.545 4. 17163.636 5. 12872.727arrow_forward
- Calculate the Von-Mises effective stress at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.27870.272 O2. 18580.181 3. 11148.109 O 4. 14864.145 O 5.22296.218arrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45°arrow_forwardA close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as σ = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>> t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. Orr T Ozz бее буг Z бее T бел Figure Q3 Centreline of the wall Rarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
EVERYTHING on Axial Loading Normal Stress in 10 MINUTES - Mechanics of Materials; Author: Less Boring Lectures;https://www.youtube.com/watch?v=jQ-fNqZWrNg;License: Standard YouTube License, CC-BY