Chapter 3, Problem 3.77HP

Many practical circuit elements are non-linear; however, it is usually possible to linearize the V-I relationship near any specific point on the non-linear V-I curve. Such a point is often referred to as an operating point. In other words, in the vicinity of an operating point $\left[V_0,I_0\right]$ the V-I relationship can be linearly approximated by:
$I=mV+B$ where $m=\text{slope}b=\mathrm{int}\text{ercept}$
The inverse to the slope m at the operating point is defined as incremental resistance $R_{inc}$ :
   $R_{inc}=\frac{dV}{dI}{\left|{}_{\left[V_0,I_0\right]}\approx \frac{\Delta V}{\Delta I}\right|}_{\left[V_0,I_0\right]}$
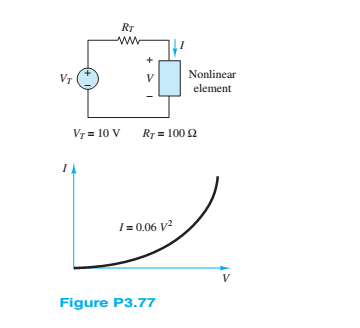
a. Refer to Figure P3.77 and find the operating point of the non-linear element.
b. Find the incremental resistance of the non-linear element at the operating point.
c. If $V_T$ is increased to 20 V, what is the new operating point and the new incremental resistance?