CALCULUS: EARLY TRANSCENDENTALS (LCPO)
3rd Edition
ISBN: 9780134856971
Author: Briggs
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 17.1, Problem 52E
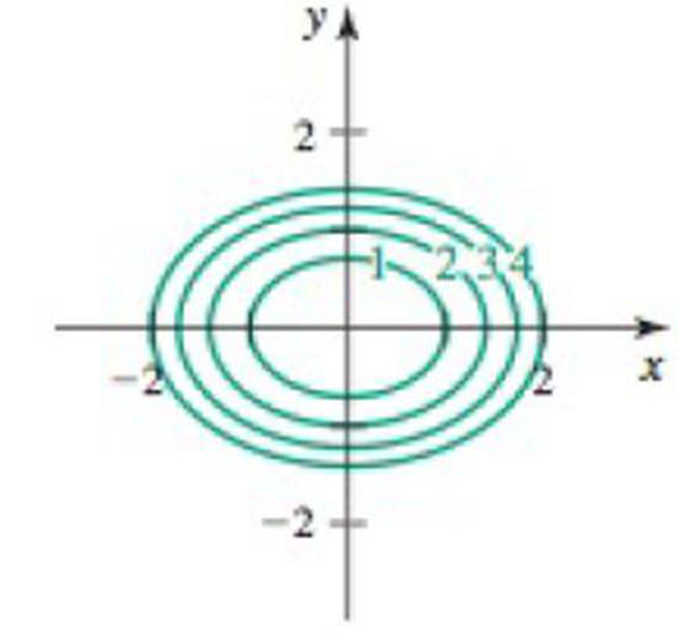
Equipotential curves Consider the following potential functions and graphs of their equipotential curves.
a. Find the associated gradient field F = ▿ϕ.
b. Show that the vector field is orthogonal to the equipotential curve at the point (1, 1). Illustrate this result on the figure.
c. Show that the vector field is orthogonal to the equipotential curve at all points (x, y).
d. Sketch two flow curves representing F that are everywhere orthogonal to the equipotential curves.
40. ϕ (x, y) = x2+ 2y2
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Determine if each of the following vector fields is the gradient of a function f(x, y). If so, find all of the
functions with this gradient.
(a) (3x² + e¹0) i + (10x e¹0 - 9 siny) j
(b) (10x el0y 9 sin y) i + (3x² + e¹0y) j
a) I have placed my work and my answer on my answer sheet
Gradient fields on curves For the potential function φ and points A, B, C, and D on the level curve φ(x, y) = 0, complete the following steps.a. Find the gradient field F = ∇φ.b. Evaluate F at the points A, B, C, and D.c. Plot the level curve φ(x, y) = 0 and the vectors F at the points A, B, C, and D.
φ(x, y) = y - 2x; A(-1, -2), B(0, 0), C(1, 2), and D(2, 4)
3. Let f(x, y) = sin x + sin y. (NOTE: You may use software for any part
of this problem.)
(a) Plot a contour map of f.
(b) Find the gradient Vf.
(c) Plot the gradient vector field Vf.
(d) Explain how the contour map and the gradient vector field are
related.
(e) Plot the flow lines of Vf.
(f) Explain how the flow lines and the vector field are related.
(g) Explain how the flow lines of Vf and the contour map are related.
Chapter 17 Solutions
CALCULUS: EARLY TRANSCENDENTALS (LCPO)
Ch. 17.1 - If the vector field in Example 1c describes the...Ch. 17.1 - In Example 2, verify that g(x, y). G(x, y) = 0. In...Ch. 17.1 - Find the gradient field associated with the...Ch. 17.1 - How is a vector field F = f, g, h used to describe...Ch. 17.1 - Sketch the vector field F = x, y.Ch. 17.1 - Prob. 3ECh. 17.1 - Given a differentiable, scalar-valued function ,...Ch. 17.1 - Interpret the gradient field of the temperature...Ch. 17.1 - Show that all the vectors in vector field...Ch. 17.1 - Sketch a few representative vectors of vector...
Ch. 17.1 - Sketching vector fields Sketch the following...Ch. 17.1 - Sketching vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Two-dimensional vector fields Sketch the following...Ch. 17.1 - Prob. 20ECh. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Three-dimensional vector fields Sketch a few...Ch. 17.1 - Matching vector Fields with graphs Match vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Normal and tangential components For the vector...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Design your own vector field Specify the component...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields on curves For the potential...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Gradient fields Find the gradient field F = for...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Equipotential curves Consider the following...Ch. 17.1 - Explain why or why not Determine whether the...Ch. 17.1 - Electric field due to a point charge The electric...Ch. 17.1 - Electric field due to a line of charge The...Ch. 17.1 - Gravitational force due to a mass The...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Flow curves in the plane Let...Ch. 17.1 - Prob. 62ECh. 17.1 - Prob. 63ECh. 17.1 - Prob. 64ECh. 17.1 - Prob. 65ECh. 17.1 - Vector fields in polar coordinates A vector field...Ch. 17.1 - Cartesian-to-polar vector field Write the vector...Ch. 17.2 - Explain mathematically why differentiating the arc...Ch. 17.2 - Suppose r(t) = t,0, for a t b, is a parametric...Ch. 17.2 - Prob. 3QCCh. 17.2 - Suppose a two dimensional force field is...Ch. 17.2 - Prob. 5QCCh. 17.2 - How does a line integral differ from the...Ch. 17.2 - If a curve C is given by r(t) = t, t2, what is...Ch. 17.2 - Prob. 3ECh. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find a parametric description r(t) for the...Ch. 17.2 - Find an expression for the vector field F = x y,...Ch. 17.2 - Suppose C is the curve r(t) = t,t3, for 0 t 2,...Ch. 17.2 - Suppose C is the circle r(l) = cos l, sin l , for...Ch. 17.2 - State two other forms for the line integral CFTds...Ch. 17.2 - Assume F is continuous on a region containing the...Ch. 17.2 - Assume F is continuous on a region containing the...Ch. 17.2 - How is the circulation of a vector field on a...Ch. 17.2 - Prob. 16ECh. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals in 3Convert the line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals in 3Convert the line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Scalar line integrals Evaluate the following line...Ch. 17.2 - Mass and density A thin wire represented by the...Ch. 17.2 - Mass and density A thin wire represented by the...Ch. 17.2 - Average values Find the average value of the...Ch. 17.2 - Average values Find the average value of the...Ch. 17.2 - Length of curves Use a scalar line integral to...Ch. 17.2 - Length of curves Use a scalar line integral to...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - Line integrals of vector fields in the plane Given...Ch. 17.2 - 47–48. Line integrals from graphs Determine...Ch. 17.2 - Line integrals from graphs Determine whether c F ...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals Given the force field F, find the...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Work integrals in 3 Given the force field F, find...Ch. 17.2 - Circulation Consider the following vector fields F...Ch. 17.2 - Circulation Consider the following vector fields F...Ch. 17.2 - Flux Consider the vector fields and curves in...Ch. 17.2 - Flux Consider the vector fields and curves in...Ch. 17.2 - Explain why or why not Determine whether the...Ch. 17.2 - Flying into a headwind An airplane flies in the...Ch. 17.2 - Flying into a headwind
How does the result of...Ch. 17.2 - Prob. 64ECh. 17.2 - Changing orientation Let f(x, y) = x and let C be...Ch. 17.2 - Work in a rotation field Consider the rotation...Ch. 17.2 - Work in a hyperbolic field Consider the hyperbolic...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Assorted line integrals Evaluate each line...Ch. 17.2 - Flux across curves in a vector field Consider the...Ch. 17.2 - Prob. 74ECh. 17.2 - Zero circulation fields 57.Consider the vector...Ch. 17.2 - Zero flux fields 58.For what values of a and d...Ch. 17.2 - Zero flux fields 59.Consider the vector field F =...Ch. 17.2 - Heat flux in a plate A square plate R = {(x, y): 0...Ch. 17.2 - Prob. 79ECh. 17.2 - Line integrals with respect to dx and dy Given a...Ch. 17.2 - Looking ahead: Area from line integrals The area...Ch. 17.2 - Prob. 82ECh. 17.3 - Is a figure-8 curve simple? Closed? Is a torus...Ch. 17.3 - Explain why a potential function for a...Ch. 17.3 - Verify by differentiation that the potential...Ch. 17.3 - Explain why the vector field (xy + xz yz) is...Ch. 17.3 - What does it mean for a function to have an...Ch. 17.3 - What are local maximum and minimum values of a...Ch. 17.3 - What conditions must be met to ensure that a...Ch. 17.3 - How do you determine whether a vector field in 3...Ch. 17.3 - Briefly describe how to find a potential function ...Ch. 17.3 - If F is a conservative vector field on a region R,...Ch. 17.3 - If F is a conservative vector field on a region R,...Ch. 17.3 - Give three equivalent properties of conservative...Ch. 17.3 - How do you determine the absolute maximum and...Ch. 17.3 - Explain how a function can have an absolute...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Testing for conservative vector fields Determine...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Finding Potential functions Determine Whether the...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Designing a function Sketch a graph of a function...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Finding potential functions Determine whether the...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Evaluating line integrals Evaluate the line...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Applying the Fundamental Theorem of Line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integrals...Ch. 17.3 - Using the Fundamental Theorem for line integral...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Line integrals of vector fields on closed curves...Ch. 17.3 - Evaluating line integral using level curves...Ch. 17.3 - Evaluating line integral using level curves...Ch. 17.3 - Line integrals Evaluate each line integral using a...Ch. 17.3 - Line integrals Evaluate each line integral using a...Ch. 17.3 - Line integrals Evaluate the following line...Ch. 17.3 - Line integrals Evaluate the following line...Ch. 17.3 - Prob. 57ECh. 17.3 - Prob. 58ECh. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Work in force fields Find the work required to...Ch. 17.3 - Suppose C is a circle centered at the origin in a...Ch. 17.3 - A vector field that is continuous in R2 is given...Ch. 17.3 - Prob. 65ECh. 17.3 - Conservation of energy Suppose an object with mass...Ch. 17.3 - Gravitational potential The gravitational force...Ch. 17.3 - Radial Fields in 3 are conservative Prove that the...Ch. 17.3 - 55.Rotation fields are usually not conservative...Ch. 17.3 - Linear and quadratic vector fields a.For what...Ch. 17.3 - Prob. 71ECh. 17.3 - Prob. 72ECh. 17.3 - Prob. 73ECh. 17.3 - Prob. 74ECh. 17.3 - Prob. 75ECh. 17.4 - Compute gxfy for the radial vector field...Ch. 17.4 - Compute fxgy for the radial vector field...Ch. 17.4 - Prob. 3QCCh. 17.4 - Explain why Greens Theorem proves that if gx = fy,...Ch. 17.4 - Explain why the two forms of Greens Theorem are...Ch. 17.4 - Referring to both forms of Greens Theorem, match...Ch. 17.4 - Prob. 3ECh. 17.4 - Why does a two-dimensional vector field with zero...Ch. 17.4 - Why does a two-dimensional vector field with zero...Ch. 17.4 - Sketch a two-dimensional vector field that has...Ch. 17.4 - Sketch a two-dimensional vector field that has...Ch. 17.4 - Discuss one of the parallels between a...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Prob. 12ECh. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Assume C is a circle centered at the origin,...Ch. 17.4 - Suppose C is the boundary of region R = {(x, y):x2...Ch. 17.4 - Suppose C is the boundary of region R = {(x, y):...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Greens Theorem, circulation form Consider the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Area of regions Use a line integral on the...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens Theorem, flux form Consider the following...Ch. 17.4 - Greens theorem, flux form Consider the following...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - 3140. Line integrals Use Greens Theorem to...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals use Greens Theorem to evaluate the...Ch. 17.4 - Line integrals Use Greens Theorem to evaluate the...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - General regions For the following vector fields,...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Circulation and flux for the following vector...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Circulation and flux For the following vector...Ch. 17.4 - Explain why or why not Determine whether the...Ch. 17.4 - Special line integrals Prove the following...Ch. 17.4 - Special line integrals Prove the following...Ch. 17.4 - Prob. 52ECh. 17.4 - Area line integral Show that the value of...Ch. 17.4 - Area line integral In terms of the parameters a...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Stream function Recall that if the vector field F...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Applications 5356. Ideal flow A two-dimensional...Ch. 17.4 - Prob. 63ECh. 17.4 - Greens Theorem as a Fundamental Theorem of...Ch. 17.4 - Greens Theorem as a Fundamental Theorem of...Ch. 17.4 - Whats wrong? Consider the rotation field...Ch. 17.4 - Whats wrong? Consider the radial field...Ch. 17.4 - Prob. 68ECh. 17.4 - Flux integrals Assume the vector field F = (f, g)...Ch. 17.4 - Streamlines are tangent to the vector field Assume...Ch. 17.4 - Streamlines and equipotential lines Assume that on...Ch. 17.4 - Channel flow The flow in a long shallow channel is...Ch. 17.5 - Show that is a vector field has the form...Ch. 17.5 - Verify the claim made in Example 3d by showing...Ch. 17.5 - Show that is a vector field has the form...Ch. 17.5 - Is (uF) a vector function or a scalar function?Ch. 17.5 - Explain how to compute the divergence of the...Ch. 17.5 - Interpret the divergence of a vector field.Ch. 17.5 - What does it mean if the divergence of a vector...Ch. 17.5 - Explain how to compute the curl of the vector...Ch. 17.5 - Interpret the curl of a general rotation vector...Ch. 17.5 - What does it mean if the curl of a vector field is...Ch. 17.5 - What is the value of ( F)?Ch. 17.5 - What is the value of u?Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of vector fields Find the divergence of...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence of radial fields Calculate the...Ch. 17.5 - Divergence and flux from graphs Consider the...Ch. 17.5 - Divergence and flux from graphs Consider the...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a rotational field Consider the following...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Curl of a vector field Compute the curl of the...Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Derivative rules Prove the following identities....Ch. 17.5 - Explain why or why not Determine whether the...Ch. 17.5 - Another derivative combination Let F = (f, g, h)...Ch. 17.5 - Does it make sense? Are the following expressions...Ch. 17.5 - Zero divergence of the rotation field Show that...Ch. 17.5 - General rotation fields a.Let a = (0, 1, 0), r =...Ch. 17.5 - Prob. 44ECh. 17.5 - Curl of the rotation field For the general...Ch. 17.5 - Inward to outward Find the exact points on the...Ch. 17.5 - Maximum divergence Within the cube {(x, y, z): |x|...Ch. 17.5 - Maximum curl Let F =
Find the scalar component of...Ch. 17.5 - Zero component of the curl For what vectors n is...Ch. 17.5 - Prob. 50ECh. 17.5 - Find a vector Field Find a vector field F with the...Ch. 17.5 - Prob. 52ECh. 17.5 - Paddle wheel in a vector field Let F = z, 0, 0 and...Ch. 17.5 - Angular speed Consider the rotational velocity...Ch. 17.5 - Angular speed Consider the rotational velocity...Ch. 17.5 - Heat flux Suppose a solid object in 3 has a...Ch. 17.5 - Heat flux Suppose a solid object in 3 has a...Ch. 17.5 - Prob. 58ECh. 17.5 - Gravitational potential The potential function for...Ch. 17.5 - Electric potential The potential function for the...Ch. 17.5 - Navier-Stokes equation The Navier-Stokes equation...Ch. 17.5 - Stream function and vorticity The rotation of a...Ch. 17.5 - Amperes Law One of Maxwells equations for...Ch. 17.5 - Prob. 64ECh. 17.5 - Properties of div and curl Prove the following...Ch. 17.5 - Prob. 66ECh. 17.5 - Identities Prove the following identities. Assume...Ch. 17.5 - Identities Prove the following identities. Assume...Ch. 17.5 - Prob. 69ECh. 17.5 - Prob. 70ECh. 17.5 - Prob. 71ECh. 17.5 - Prob. 72ECh. 17.5 - Prob. 73ECh. 17.5 - Gradients and radial fields Prove that for a real...Ch. 17.5 - Prob. 75ECh. 17.6 - Describe the surface r(u, v) = 2cosu,2sinu,v,for 0...Ch. 17.6 - Describe the surface r(u, v) = vcosu,vsinu,v, for...Ch. 17.6 - Describe the surface r(u, v) =...Ch. 17.6 - Prob. 4QCCh. 17.6 - Explain why explicit description for a cylinder x2...Ch. 17.6 - Explain why the upward flux for the radial field...Ch. 17.6 - Give a parametric description for a cylinder with...Ch. 17.6 - Prob. 2ECh. 17.6 - Give a parametric description for a sphere with...Ch. 17.6 - Prob. 4ECh. 17.6 - Explain how to compute the surface integral of a...Ch. 17.6 - Explain what it means for a surface to be...Ch. 17.6 - Describe the usual orientation of a closed surface...Ch. 17.6 - Why is the upward flux of a vertical vector field...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Parametric descriptions Give a parametric...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Identify the surface Describe the surface with the...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface area using a parametric description Find...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface integrals using a parametric description...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface area using an explicit description Find...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Surface integrals using an explicit description...Ch. 17.6 - Average Values 39. Find the average temperature on...Ch. 17.6 - Average values 40.Find the average squared...Ch. 17.6 - Average values 41.Find the average value of the...Ch. 17.6 - Average values 42.Find the average value of the...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Surface integrals of vector fields Find the flux...Ch. 17.6 - Explain why or why not Determine whether the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Miscellaneous surface integrals Evaluate the...Ch. 17.6 - Cone and sphere The cone z2 = x2 + y2 for z 0,...Ch. 17.6 - Cylinder and sphere Consider the sphere x2 + y2 +...Ch. 17.6 - Flux on a tetrahedron Find the upward flux of the...Ch. 17.6 - Flux across a cone Consider the field F = x, y, z...Ch. 17.6 - Surface area formula for cones Find the general...Ch. 17.6 - Surface area formula for spherical cap A sphere of...Ch. 17.6 - Radial fields and spheres Consider the radial...Ch. 17.6 - Heat flux The heat flow vector field for...Ch. 17.6 - Heat flux The heat flow vector field for...Ch. 17.6 - Prob. 63ECh. 17.6 - Flux across a cylinder Let S be the cylinder x2 +...Ch. 17.6 - Flux across concentric spheres Consider the radial...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Mass and center of mass Let S be a surface that...Ch. 17.6 - Outward normal to a sphere Show that...Ch. 17.6 - Special case of surface integrals of scalar-valued...Ch. 17.6 - Surfaces of revolution Suppose y = f(x) is a...Ch. 17.6 - Rain on roofs Let z = s(x, y) define a surface...Ch. 17.6 - Surface area of a torus a.Show that a torus with...Ch. 17.6 - Surfaces of revolution single variable Let f be...Ch. 17.7 - Suppose S is a region in the xy-plane with a...Ch. 17.7 - In Example 3a We used the parameterization r(t) =...Ch. 17.7 - In Example 4, explain why a paddle wheel with its...Ch. 17.7 - Explain the meaning of the integral S(F)ndS in...Ch. 17.7 - Explain the meaning of the integral S(F)ndS in...Ch. 17.7 - Explain the meaning of Stokes Theorem.Ch. 17.7 - Why does a conservative vector field produce zero...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Verifying Stokes Theorem Verify that the line...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating line integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Stokes Theorem for evaluating surface integrals...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Interpreting and graphing the curl For the...Ch. 17.7 - Explain why or why not Determine whether the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Conservative fields Use Stokes Theorem to find the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Tilted disks Let S be the disk enclosed by the...Ch. 17.7 - Prob. 38ECh. 17.7 - Circulation in a plane A circle C in the plane x +...Ch. 17.7 - No integrals Let F = (2z, z, 2y + x) and let S be...Ch. 17.7 - Compound surface and boundary Begin with the...Ch. 17.7 - Ampres Law The French physicist AndrMarie Ampre...Ch. 17.7 - Maximum surface integral Let S be the paraboloid z...Ch. 17.7 - Area of a region in a plane Let R be a region in a...Ch. 17.7 - Choosing a more convenient surface The goal is to...Ch. 17.7 - Radial fields and zero circulation Consider the...Ch. 17.7 - Zero curl Consider the vector field...Ch. 17.7 - Average circulation Let S be a small circular disk...Ch. 17.7 - Proof of Stokes Theorem Confirm the following step...Ch. 17.7 - Stokes Theorem on closed surfaces Prove that if F...Ch. 17.7 - Rotated Greens Theorem Use Stokes Theorem to write...Ch. 17.8 - Interpret the Divergence Theorem in the case that...Ch. 17.8 - In Example 3. does the vector field have negative...Ch. 17.8 - Draw unit cube D = {(x, y, z) : 0 x 1, 0 y 1, 0...Ch. 17.8 - Review Questions 1.Explain the meaning of the...Ch. 17.8 - Interpret the volume integral in the Divergence...Ch. 17.8 - Explain the meaning of the Divergence Theorem.Ch. 17.8 - What is the net outward flux of the rotation field...Ch. 17.8 - What is the net outward flux of the radial field F...Ch. 17.8 - What is the divergence of an inverse square vector...Ch. 17.8 - Suppose div F = 0 in a region enclosed by two...Ch. 17.8 - If div F 0 in a region enclosed by a small cube,...Ch. 17.8 - Verifying the Divergence Theorem Evaluate both...Ch. 17.8 - F = x, y, z; D = {(x, y, z): |x| 1, |y| 1, |z| ...Ch. 17.8 - Basic Skills 912.Verifying the Divergence Theorem...Ch. 17.8 - F = x2, y2, z2; D = {(x, y, z): |x| 1, |y| 2,...Ch. 17.8 - Rotation fields 13.Find the net outward flux of...Ch. 17.8 - Rotation fields 14.Find the net outward flux of...Ch. 17.8 - Find the net outward flux of the field F = bz cy,...Ch. 17.8 - Rotation fields 16.Find the net outward flux of F...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - F = x, 2y, z; S is the boundary of the tetrahedron...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - F = y 2x, x3 y, y2 z; S is the sphere {(x, y,...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Computing flux Use the Divergence Theorem to...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - F = x2, y2, z2); D is the region in the first...Ch. 17.8 - Divergence Theorem for more general regions Use...Ch. 17.8 - Explain why or why not Determine whether the...Ch. 17.8 - Flux across a sphere Consider the radial field F =...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Flux integrals Compute the outward flux of the...Ch. 17.8 - Radial fields Consider the radial vector field...Ch. 17.8 - Singular radial field Consider the radial field...Ch. 17.8 - Logarithmic potential Consider the potential...Ch. 17.8 - Gauss Law for electric fields The electric field...Ch. 17.8 - Gauss Law for gravitation The gravitational force...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Heat transfer Fouriers Law of heat transfer (or...Ch. 17.8 - Inverse square fields are special Let F be a...Ch. 17.8 - A beautiful flux integral Consider the potential...Ch. 17.8 - Integration by parts (Gauss' Formula) Recall the...Ch. 17.8 - Prob. 49ECh. 17.8 - Prob. 50ECh. 17.8 - Greens Second Identity Prose Greens Second...Ch. 17.8 - Prob. 52ECh. 17.8 - Prob. 53ECh. 17.8 - Prob. 54ECh. 17 - Explain why or why not Determine whether the...Ch. 17 - Matching vector fields Match vector fields a-f...Ch. 17 - Gradient fields in 2 Find the vector field F = ...Ch. 17 - Gradient fields in 2 Find the vector field F = ...Ch. 17 - Gradient fields in 3 Find the vector field F = ...Ch. 17 - Gradient fields in 3 Find the vector field F = ...Ch. 17 - Normal component Let C be the circle of radius 2...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Line integrals Evaluate the following line...Ch. 17 - Two parameterizations Verify that C(x2y+3z)ds has...Ch. 17 - Work integral Find the work done in moving an...Ch. 17 - Work integrals in R3 Given the following force...Ch. 17 - Work integrals in 3 Given the following force...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Circulation and flux Find the circulation and the...Ch. 17 - Flux in channel flow Consider the flow of water in...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Conservative vector fields and potentials...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Evaluating line integrals Evaluate the line...Ch. 17 - Radial fields in R2 are conservative Prove that...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Greens Theorem for line integrals Use either form...Ch. 17 - Areas of plane regions Find the area of the...Ch. 17 - Areas of plane regions Find the area of the...Ch. 17 - Circulation and flux Consider the following vector...Ch. 17 - Circulation and flux Consider the following vector...Ch. 17 - Parameters Let F = ax + by, cx + dy, where a, b,...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Divergence and curl Compute the divergence and...Ch. 17 - Identities Prove that (1|r|4)=4r|r|6 and use the...Ch. 17 - Maximum curl Let F=z,x,y. a. What is the scalar...Ch. 17 - Paddle wheel in a vector field Let F = 0, 2x, 0...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface areas Use a surface integral to find the...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Surface integrals Evaluate the following surface...Ch. 17 - Flux integrals Find the flux of the following...Ch. 17 - Flux integrals Find the flux of the following...Ch. 17 - Three methods Find the surface area of the...Ch. 17 - Flux across hemispheres and paraboloids Let S be...Ch. 17 - Surface area of an ellipsoid Consider the...Ch. 17 - Stokes Theorem for line integrals Evaluate the...Ch. 17 - Stokes Theorem for line integrals Evaluate the...Ch. 17 - Stokes Theorem for surface integrals Use Stokes...Ch. 17 - Stokes Theorem for surface integrals Use Stokes...Ch. 17 - Conservative fields Use Stokes Theorem to find the...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - Computing fluxes Use the Divergence Theorem to...Ch. 17 - General regions Use the Divergence Theorem to...Ch. 17 - General regions Use the Divergence Theorem to...Ch. 17 - Flux integrals Compute the outward flux of the...Ch. 17 - Stokes Theorem on a compound surface Consider the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Assessment 1-1A The following is a magic square all rows, columns, and diagonals sum to the same number. Find t...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
2. Reported Versus Measured In a survey of 1046 adults conducted by Bradley Corporation, subjects were asked ho...
Elementary Statistics (13th Edition)
Matching In Exercises 17–20, match the level of confidence c with the appropriate confidence interval. Assume e...
Elementary Statistics: Picturing the World (7th Edition)
Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...
A First Course in Probability (10th Edition)
Cylinder and paraboloids Find the volume of the region bounded below by the paraboloid z = x2 + y2, laterally b...
University Calculus: Early Transcendentals (4th Edition)
Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...
College Algebra (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Plz solve part carrow_forwardFind the gradient fields ƒ(x, y, z) = (x raise to the power 2 + y raise to the power 2 + z raise to the power 2)-1>2arrow_forwardA net is dipped in a river. Determine the flow rate of water across the net if the velocity vector field for the river is given by v = (x - y, z + y +7,z²) and the net is decribed by the equation y = √1-x²-2², y 20, and oriented in the positive y-direction. (Use symbolic notation and fractions where needed.) 1.45-1 yasarrow_forward
- The vector function r(t) is the position of a particle in space at time t. Determine the graph of the position function. r(t) = (3t cos t)i + (3t sin t)j + 2tkarrow_forwardFourier's Law of heat transfer (or heat conduction) states that the heat flow vector F at a point is proportional to the negative gradient of the temperature: that is, F= -kVT, which means that heat energy flows from hot regions to cold regions. The constant k is called the conductivity, which has metric units of J/m-s-K or W/m-K. A temperature function T for a region D is given below. Find the net outward heat flux SSF•nds= - kff triple integral. Assume that k = 1. T(x,y,z)=110e-x²-y²-2². D is the sphere of radius a centered at the origin. The net outward heat flux across the boundary is. (Type an exact answer, using as needed.) G S VT.n dS across the boundary S of D. It may be easier to use the Divergence Theorem and evaluate aarrow_forward7. Properties of position vectors Let r = xi + yj + zk and let r = |r|. a. Show that Vr = r/r. b. Show that V(r") = nr"-2r. c. Find a function whose gradient equals r.arrow_forward
- a. Sketch the graph of r(t) = ti+t2j. Show that r(t) is a smooth vector-valued function but the change of parameter t = 73 produces a vector-valued function that is not smooth, yet has the same graph as r(t). b. Examine how the two vector-valued functions are traced, and see if you can explain what causes the problem.arrow_forwardEasy Calculus, please solve. I will rate and like. Thank you.arrow_forwardRepresent the curve by a vector-valued function r(t) using the given parameter.arrow_forward
- Sketch the plane curve represented by the vector-valued function and give the orientation of the curve. r(t) = i + (t− 1)j eBook -10 -10 O -5 -5 y 10 5 -fol y 10 5 -105 5 5 10 X X 10 -10 -10 -5 -5 y 10 5 -fol y 10 5 -104 5 5 X 10 X 10arrow_forwardFourier's Law of heat transfer (or heat conduction) states that the heat flow vector F at a point is proportional to the negative gradient of the temperature: that is, F = -kVT, which means that heat energy flows from hot regions to cold regions. The constant k is called FondSk the conductivity, which has metric units of J/m-s-K or W/m-K. A temperature function T for a region D is given below. Find the net outward heat fluxarrow_forwardplease send correct answerarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY