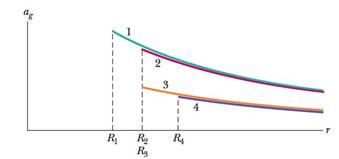
Problem 1Q: In Fig. 13-21, a central particle of mass M is surrounded by a square array of other particles,... Problem 2Q Problem 3Q: In Fig. 13-23, a central particle is surrounded by two circular rings of particles, at radii r and... Problem 4Q: In Fig. 13-24, two particles, of masses m and 2m, are fixed in place on an axis, a Where on the axis... Problem 5Q Problem 6Q: In Fig. 13-26, three particles are fixed in place. The mass of B is greater than the mass of C. Can... Problem 7Q: Rank the four systems of equal- mass particles shown in Checkpoint 2 according to the absolute value... Problem 8Q: Figure 13-27 gives the gravitational acceleration ag for four planets as a function of the radial... Problem 9Q: Figure 13-28 shows three particles initially fixed in place, with B and C identical and positioned... Problem 10Q: Figure 13-29 shows six paths by which a rocket orbiting a moon might move from point a to point b.... Problem 11Q: Figure 13-30 shows three uniform spherical planets that are identical in size and mass. The periods... Problem 12Q: In Fig. 13-31, a particle of mass m which is not shown is to be moved from an infinite distance to... Problem 1P: ILW A mass M is split into two parts, m and M m, which are then separated by a certain distance.... Problem 2P: Moon effect. Some people believe that the Moon controls their activities. If the Moon moves from... Problem 3P Problem 4P: The Sun and Earth each exert a gravitational force on the Moon. What is the ratio FSun/FEarth of... Problem 5P: Miniature black holes. Left over from the big-bang beginning of the universe, tiny black holes might... Problem 6P: GO In Fig. 13-32, a square of edge length 20.0 cm is formed by four spheres of masses m1 = 5.00 g,... Problem 7P: One dimension. In Fig. 13-33, two point particles are fixed on an x axis separated by distance d,... Problem 8P: In Fig. 13-34, three 5.00 kg spheres are located at distances d1 = 0.300 m and d2 = 0.400 m. What... Problem 9P: SSM WWW We want to position a space probe along a line that extends directly toward the Sun in order... Problem 10P Problem 11P: As seen in Fig. 13-36, two spheres of mass m and a third sphere of mass M form an equilateral... Problem 12P: GO In Fig. 13-37a, particle A is fixed in place at x = 0.20 m on the x axis and particle B. with a... Problem 13P: Figure 13-38 shows a spherical hollow inside a lead sphere of radius R = 4.00 cm; the surface of the... Problem 14P Problem 15P: GO Three dimensions. Three point particles are fixed in place in an xyz coordinate system. Particle... Problem 16P: GO In Fig. 13-40, a particle of mass m1 = 0.67 kg is a distance d = 23 cm from one end of a uniform... Problem 17P: a What will an object weigh on the Moons surface if it weighs 100 N on Earths surface? b How many... Problem 18P: Mountain pull. A large mountain can slightly affect the direction of down as determined by a plumb... Problem 19P: SSM At what altitude above Earths surface would the gravitational acceleration be 4.9 m/s2? Problem 20P: Mile-high building. In 1956, Frank Lloyd Wright proposed the construction of a mile-high building in... Problem 21P: ILW Certain neutron stars extremely dense stars are believed to be rotating at about l rev/s. If... Problem 22P Problem 23P Problem 24P: Two concentric spherical shells with uniformly distributed masses M1and M2 are situated as shown in... Problem 25P: A solid sphere has a uniformly distributed mass of 1.0 104 kg and a radius of 1.0 m. What is the... Problem 26P Problem 27P: Figure 13-42 shows, not to scale, a cross section through the interior of Earth. Rather than being... Problem 28P Problem 29P Problem 30P: In Problem 1, what ratio m/M gives the least gravitational potential energy for the system? Problem 31P: SSM The mean diameters of Mars and Earth are 6.9 103 km and 13 104 km, respectively. The mass of... Problem 32P: a What is the gravitational potential energy of the two-particle system in Problem 3? If you triple... Problem 33P Problem 34P Problem 35P: GO Figure 13-44 shows four particles, each of mass 20.0 g, that form a square with an edge length of... Problem 36P: Zero, a hypothetical planet, has a mass of 5.0 1023 kg, a radius of 3.0 106 m, and no atmosphere.... Problem 37P: GO The three spheres in Fig, 13-45, with masses mA = 80 g, mB = 10 g, and mC = 20 g, have their... Problem 38P: In deep space, sphere A of mass 20 kg is located at the origin of an x axis and sphere B of mass 10... Problem 39P Problem 40P: A projectile is shot directly away from Earths surface. Neglect the rotation of Earth. What multiple... Problem 41P: SSM Two neutron stars arc separated by a distance of 1.0 1010 m. They each have a mass of 1.0 1030... Problem 42P: GO Figure 13-46a shows a particle A that can he moved along a y axis from an infinite distance to... Problem 43P: a What linear speed must an Earth satellite have to he in a circular orbit al an altitude of 160 km... Problem 44P Problem 45P: The Martian satellite Photos travels in an approximately circular orbit of radius 9.4 106 m with a... Problem 46P: The first known collision between space debris and a functioning satellite occurred in 1996: At an... Problem 47P Problem 48P: The mean distance of Mars from the Sun is 1.52 Limes that of Earth from the Sun. From Keplers law of... Problem 49P Problem 50P Problem 51P Problem 52P: The Suns center is at one focus of Earths orbit. How far from this focus is the other focus, a in... Problem 53P: A 20 kg satellite has a circular orbit with a period of 2.4 h and a radius of 8.0 106m around a... Problem 54P Problem 55P: In 1610, Galileo used his telescope to discover four moons around Jupiter, with these mean orbital... Problem 56P: In 1993 the spacecraft Galileo sent an image Fig. 13-48 of asteroid 243 Ida and a tiny orbiting moon... Problem 57P Problem 58P Problem 59P: Three identical stars of mass M form an equilateral triangle that rotates around the triangles... Problem 60P: In Fig. 13-50, two satellites, A and B, both of mass m = 125 kg, move in the same circular orbit of... Problem 61P Problem 62P Problem 63P: SSM WWW An asteroid, whose mass is 2.0 10-4 times the mass of Earth, revolves in a circular orbit... Problem 64P: A satellite orbits a planet of unknown mass in a circle of radius 2.0 107 m. The magnitude of the... Problem 65P: A Satellite is in a circular Earth orbit of radius r. The area A enclosed by the orbit depends on r2... Problem 66P: One way to attack a satellite in Earth orbit is to launch a swarm of pellets in the same orbit as... Problem 67P Problem 68P: GO Two small spaceships, each with mass m = 2000 kg, are in the circular Earth orbit of Fig. 13-51,... Problem 69P Problem 70P Problem 71P: Several planets Jupiter. Saturn, Uranus are encircled by rings, perhaps composed of material that... Problem 72P Problem 73P: Figure 13-53 is a graph of the kinetic energy K of an asteroid versus its distance r from Earths... Problem 74P: The mysterious visitor that appears in the enchanting story The Little Prince was said to come from... Problem 75P: ILW The masses and coordinates of three spheres are as follows; 20 kg, x = 0.50 m, y = 1.0 m; 40 kg,... Problem 76P: SSM A very early, simple satellite consisted of an inflated spherical aluminum balloon 30 m in... Problem 77P: GO Four uniform spheres, with masses mA = 40 kg, mB = 35 kg, mC = 200 kg, and mD = 50 kg, have x, y... Problem 78P: a In Problem 77, remove sphere A and calculate the gravitational potential energy of the remaining... Problem 79P Problem 80P Problem 81P Problem 82P Problem 83P Problem 84P Problem 85P Problem 86P Problem 87P Problem 88P Problem 89P Problem 90P: A 50 kg satellite circles planet Cruton every 6.0 h. The magnitude of the gravitation a I farce... Problem 91P Problem 92P: A 150.0 kg rocket moving radially outward from Earth has a speed of 3.70 km/c when its engine shuts... Problem 93P Problem 94P: Two 20 kg spheres are fixed in place on a y axis, one at y = 0.40 m and the other at y = 0.40 m. A... Problem 95P: Sphere A with mass 80 kg is located at the origin of an xy coordinate system; sphere B with mass 60... Problem 96P: In his 1865 science fiction novel From the Earth to the Moon Jules Verne described how three... Problem 97P Problem 98P Problem 99P: A thin rod with mass M = 5.00 kg is bent in a semicircle of radius R = 0.650 m Fig. 13-56. a What is... Problem 100P: In Fig. 13-57, identical blocks with identical masses m = 2.00 kg hang from strings of different... Problem 101P: A spaceship is on a straight-line path between Earth and the Moon. At what distance from Earth is... format_list_bulleted


 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




