
(a)
Interpretation:
The given statements have to be answered.
Concept Introduction:
The time taken by the concentration of reaction to get reduced of its original concentration is called as half-life reaction.
Half life for first order reactions:
The half life for the first order reaction is constant and it is independent of the reactant concentration.
Half life period of first order reaction can be calculated using the equation,
Half life for second order reactions:
In second order reaction, the half-life is inversely proportional to the initial concentration of the reactant (A).
The half-life of second order reaction can be calculated using the equation,
Since the reactant will be consumed in lesser amount of time, these reactions will have shorter half-life.
To complete the pictures
(a)
Explanation of Solution
The reaction follows first order with presence of half-life of ten seconds.
There are 16 AB particles present in the container,
After one half life (10s) 8 particles will be reacted and 8 remains unreacted.
After two-half lives (20s) 12 particles will be reacted and 4 remains unreacted.
The completed pictures are,
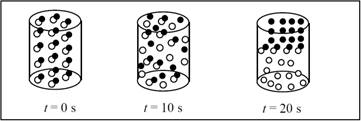
Figure 1
(b)
Interpretation:
The given statements have to be answered.
Concept Introduction:
The time taken by the concentration of reaction to get reduced of its original concentration is called as half-life reaction.
Half life for first order reactions:
The half life for the first order reaction is constant and it is independent of the reactant concentration.
Half life period of first order reaction can be calculated using the equation,
Half life for second order reactions:
In second order reaction, the half-life is inversely proportional to the initial concentration of the reactant (A).
The half-life of second order reaction can be calculated using the equation,
Since the reactant will be consumed in lesser amount of time, these reactions will have shorter half-life.
To explain the changes in completed figure if the reaction was second-order with same half life
(b)
Explanation of Solution
If the half-life is similar for second-order reaction, the container t=20s would have more number of AB and fewer A and B when compared to part a.
(c)
Interpretation:
The given statements have to be answered.
Concept Introduction:
The time taken by the concentration of reaction to get reduced of its original concentration is called as half-life reaction.
Half life for first order reactions:
The half life for the first order reaction is constant and it is independent of the reactant concentration.
Half life period of first order reaction can be calculated using the equation,
Half life for second order reactions:
In second order reaction, the half-life is inversely proportional to the initial concentration of the reactant (A).
The half-life of second order reaction can be calculated using the equation,
Since the reactant will be consumed in lesser amount of time, these reactions will have shorter half-life.
To give the relative
(c)
Explanation of Solution
After 10 seconds, the concentration of the particles is one-half their initial value. Then relative rate of reactions for first-order at the start and after 10 seconds are,
(d)
Interpretation:
The given statements have to be answered.
Concept Introduction:
The time taken by the concentration of reaction to get reduced of its original concentration is called as half-life reaction.
Half life for first order reactions:
The half life for the first order reaction is constant and it is independent of the reactant concentration.
Half life period of first order reaction can be calculated using the equation,
Half life for second order reactions:
In second order reaction, the half-life is inversely proportional to the initial concentration of the reactant (A).
The half-life of second order reaction can be calculated using the equation,
Since the reactant will be consumed in lesser amount of time, these reactions will have shorter half-life.
To give the relative reaction rates for second order reaction at the start of reaction and after 10 seconds elapsed
(d)
Explanation of Solution
After 10 seconds, the concentration of the particles is one-half their initial value. Then relative rate of reactions for second order at the start and after 10 seconds are,
Want to see more full solutions like this?
Chapter 13 Solutions
General Chemistry - Standalone book (MindTap Course List)
- Iarrow_forwardDraw the Markovnikov product of the hydrobromination of this alkene. Note for advanced students: draw only one product, and don't worry about showing any stereochemistry. Drawing dash and wedge bonds has been disabled for this problem. + Explanation Check 1 X E 4 1 1 1 1 1 HBr Click and drag to start drawing a structure. 80 LE #3 @ 2 $4 0 I அ2 % 85 F * K M ? BH 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use Privacy Center & 6 27 FG F10 8 9 R T Y U D F G H P J K L Z X C V B N M Q W A S H option command H command optiarrow_forwardBe sure to use wedge and dash bonds to show the stereochemistry of the products when it's important, for example to distinguish between two different major products. Predict the major products of the following reaction. Explanation Q F1 A Check F2 @ 2 # 3 + X 80 F3 W E S D $ 4 I O H. H₂ 2 R Pt % 05 LL ee F6 F5 T <6 G Click and drag to start drawing a structure. 27 & A 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use Privacy Center Acce Y U H DII 8 9 F10 4 J K L Z X C V B N M T H option command F11 P H commandarrow_forward
- Curved arrows are used to illustrate the flow of electrons. Use the reaction conditions provided and follow the arrows to draw the intermediate and product in this reaction or mechanistic step(s). Include all lone pairs and charges as appropriate. Ignore stereochemistry. Ignore inorganic byproducts. H :0: CH3 O: OH Q CH3OH2+ Draw Intermediate protonation CH3OH CH3OH nucleophilic addition H Draw Intermediate deprotonation :0: H3C CH3OH2* protonation H 0: H CH3 H.arrow_forwardPredicting the reactants or products of hemiacetal and acetal formation uentify the missing organic reactants in the following reaction: H+ X+Y OH H+ за Note: This chemical equation only focuses on the important organic molecules in the reaction. Additional inorganic or small-molecule reactants or products (like H2O) are not shown. In the drawing area below, draw the skeletal ("line") structures of the missing organic reactants X and Y. You may draw the structures in any arrangement that you like, so long as they aren't touching. Explanation Check Click and drag to start drawing a structure. ? olo 18 Ar © 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibilityarrow_forwardcan someone please answer thisarrow_forward
- Please, please help me figure out the the moles, molarity and Ksp column. Step by step details because I've came up with about three different number and have no idea what I'm doing wrong.arrow_forwardwhat reagents are used to get this product from this reactant? Br OCH3arrow_forwardcan someone answer this pleasearrow_forward
- can someone do the reaction mechanism for this reaction and draw the molecules for Q2 and q3arrow_forwardIn this question, the product of the aldol condensation is shown. What would be the reactants for this product? Please provide a detailed explanation, as well as a drawing showing how the reactants will react to produce the product.arrow_forward7. Propene undergoes a hydration reaction with water in the presence of an acid. a. There are two possible products for this reaction, both with the formula C,H,O. Show their structural formulas and names. (A1, B2) SCH4UR Name: (answer for part a. here!) VER 3 2021-2022 b. Which of the two products do you predict will form. Explain your choice using details from your learning. (B3)arrow_forward
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,Chemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,Chemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning





