Vector Mechanics for Engineers: Dynamics

11th Edition

ISBN: 9780077687342

Author: Ferdinand P. Beer, E. Russell Johnston Jr., Phillip J. Cornwell, Brian Self

Publisher: McGraw-Hill Education

See similar textbooks

Concept explainers

Power Transmission Elements

It is defined as the energy transfer from one location to another location. The energy will start moving from the energy generation source to the energy applied position to obtain the work output. From this method, a large amount of electric energy moves…

Videos

Textbook Question

Chapter 12.2, Problem 12.92P

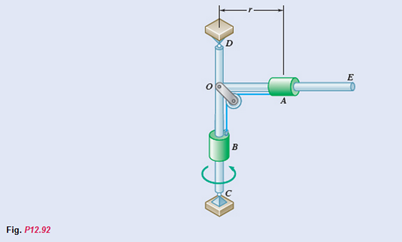
Two 2.6-Ib collars A and B can slide without friction on a frame, consisting of the horizontal rod OE and the vertical rod CD, which is free to rotate about CD. The two collars are connected by a cord running over a pulley that is attached to the frame at O, and a stop prevents collar B from moving. The frame is rotating at the rate θ ' = 12 rad/s and r = 0.6 ft when the stop is removed, allowing collar A to move out along rod OE Neglecting friction and the mass of the frame, determine, for the position r = 1.2 ft, (a) the transverse component of the velocity of collar A, (b) the tension in the cord and the acceleration of collar A relative to the rod OE.

Chapter 12.2, Problem 12.92P, Two 2.6-Ib collars A and B can slide without friction on a frame, consisting of the horizontal rod

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 12.2, Problem 12.91P

Chapter 12.2, Problem 12.93P

Students have asked these similar questions

First monthly exam Gas dynamics Third stage Q1/Water at 15° C flow through a 300 mm diameter riveted steel pipe, E-3 mm with a head loss of 6 m in 300 m length. Determine the flow rate in pipe. Use moody chart. Q2/ Assume a car's exhaust system can be approximated as 14 ft long and 0.125 ft-diameter cast-iron pipe ( = 0.00085 ft) with the equivalent of (6) regular 90° flanged elbows (KL = 0.3) and a muffler. The muffler acts as a resistor with a loss coefficient of KL= 8.5. Determine the pressure at the beginning of the exhaust system (pl) if the flowrate is 0.10 cfs, and the exhaust has the same properties as air.(p = 1.74 × 10-3 slug/ft³, u= 4.7 x 10-7 lb.s/ft²) Use moody chart (1) MIDAS Kel=0.3 Q3/Liquid ammonia at -20°C is flowing through a 30 m long section of a 5 mm diameter copper tube(e = 1.5 × 10-6 m) at a rate of 0.15 kg/s. Determine the pressure drop and the head losses. .μ= 2.36 × 10-4 kg/m.s)p = 665.1 kg/m³

2/Y Y+1 2Cp Q1/ Show that Cda Az x P1 mactual Cdf Af R/T₁ 2pf(P1-P2-zxgxpf) Q2/ A simple jet carburetor has to supply 5 Kg of air per minute. The air is at a pressure of 1.013 bar and a temperature of 27 °C. Calculate the throat diameter of the choke for air flow velocity of 90 m/sec. Take velocity coefficient to be 0.8. Assume isentropic flow and the flow to be compressible. Quiz/ Determine the air-fuel ratio supplied at 5000 m altitude by a carburetor which is adjusted to give an air-fuel ratio of 14:1 at sea level where air temperature is 27 °C and pressure is 1.013 bar. The temperature of air decreases with altitude as given by the expression The air pressure decreases with altitude as per relation h = 19200 log10 (1.013), where P is in bar. State any assumptions made. t = ts P 0.0065h

36 2) Use the method of MEMBERS to determine the true magnitude and direction of the forces in members1 and 2 of the frame shown below in Fig 3.2. 300lbs/ft member-1 member-2 30° Fig 3.2. https://brightspace.cuny.edu/d21/le/content/433117/viewContent/29873977/View

Chapter 12 Solutions

Vector Mechanics for Engineers: Dynamics

Ch. 12.1 - A 1000-Ib boulder B is resting on a 200-Ib...Ch. 12.1 - Marble A is placed in a hollow tube, and the tube...Ch. 12.1 - The two systems shown start from rest. On the...Ch. 12.1 - Prob. 12.CQ4P Ch. 12.1 - People sit on a Ferris wheel at points A, B, C,...Ch. 12.1 - Crate A is gently placed with zero initial...Ch. 12.1 - Prob. 12.F2P Ch. 12.1 - Objects A, B, and C have masses mA, mB, and...Ch. 12.1 - Blocks A and B have masses mAand mB, my...Ch. 12.1 - Blocks A and B have masses mAand mB, my...

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.