Chapter 11.8, Problem 12PSC

To determine

To calculate:Thearea of pentagonABCDE .

Answer to Problem 12PSC

Thearea of pentagon ABCDEis $56.5$ .

Explanation of Solution

Given information:

In pentagon ABCDE ,

Side $AB=BC=CD=5,$

Side $ED=6,$

Side $AD=10,$

Side $AE=8.$

Formula used:

Brahmagupta’sformula is used to find the area of any cyclic quadrilateral given the length of sides.

The semi perimeter of quadrilateral is

  $s=\frac{a+b+c+d}{2}$

where a , b , c and d are sides of quadrilateral.

The area of quadrilateral is

  $A=\sqrt{(s-a)(s-b)(s-c)(s-d)}$

where a , b , c and d are sides of quadrilateraland s is semi perimeter of quadrilateral.

We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.

The semi perimeter of triangle is

  $d=\frac{x+y+z}{2}$

where x , y , and z are sides of triangle.

  $A=\sqrt{d(d-x)(d-y)(d-z)}$

where x , y , and z are sides of triangle and d is semi perimeter of triangle.

Calculation:

  

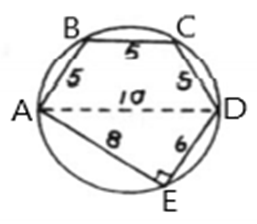
In ΔAED,

By heron’s formula, we get

  $d=\frac{AE+ED+AD}{2}=\frac{8+6+10}{2}=12$

Area of ΔAED :

  $\begin{array}{l}A=\sqrt{12(12-8)(12-6)(12-10)}\\ A=\sqrt{12\times 4\times 6\times 2}\\ A=\sqrt{576}\\ A=24\end{array}$

In quadrilateralABCD,

By Brahmagupta’sformula, we get

  $s=\frac{AB+BC+CD+AD}{2}=\frac{5+5+5+10}{2}=12.5$

Area of quadrilateral ABCD :

  $\begin{array}{l}A=\sqrt{(12.5-5)(12.5-5)(12.5-5)(12.5-10)}\\ A=\sqrt{7.5\times 7.5\times 7.5\times 2.5}\\ A=\sqrt{1054.68}\\ A\approx 32.5\end{array}$

Area of pentagon ABCDE =Area of ΔAED +Area of QuadrilateralABCD

Area of pentagon ABCDE $=24+32.5\approx 56.5$