Chapter 11, Problem 26RP

a.

To determine

To calculate: The area ratio of whole region ABC and shaded region ADC .

Answer to Problem 26RP

The area ratio is $2:1$ .

Explanation of Solution

Given information:

Side AB = 5,

Side AC = 9.

Formula used:

Area of triangle: $A=\frac{1}{2}\times b\times h$

b = base of triangle

h = height of triangle

Calculation:

  

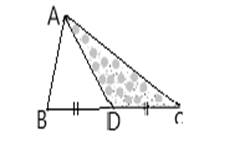
The height of both triangles is the same. If the base of a triangle is bisected and a shaded triangle has a base x, then base of whole triangle = 2x.

The area ratio is as follows:

  $\frac{A_{WholeTriangle}}{A_{ShadedTriangle}}=\frac{\frac{1}{2}\times 2x\times h}{\frac{1}{2}\times x\times h}=\frac{2}{1}$

b.

To determine

To find: The area ratio of whole region DEF and shaded region DGF .

Answer to Problem 26RP

The area ratio is $7:5$ .

Explanation of Solution

Given information:

Side DE = 2,

Side EG = x ,

Side GF = 3,

Side DF = 5.

Formula used:

The below theorem is used:

Angle bisector theorem states that “If a ray bisects an angle of a triangle, then it divides the opposite side of the triangle into segments that are proportional to the other two sides”.

  

  $\frac{a}{c}=\frac{b}{d}$

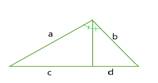
Area of triangle: $A=\frac{1}{2}\times b\times h$

b = base of triangle

h = height of triangle

Calculation:

  

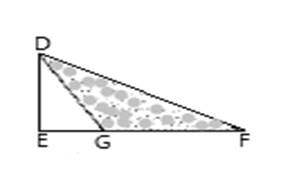
Using Angle Bisector Theorem

  $\begin{array}{l}\frac{2}{x}=\frac{5}{3}\\ 5x=6\\ x=\frac{6}{5}\end{array}$

The base of whole triangle $=x+3$

Base $=\frac{6}{5}+3=\frac{21}{5}$

The height of both triangles is the same, so the height of each can be set equal to h .

  $\frac{A_{WholeTriangle}}{A_{ShadedTriangle}}=\frac{\frac{1}{2}\times \frac{21}{5}\times h}{\frac{1}{2}\times \frac{15}{5}\times h}=\frac{21}{15}=\frac{7}{5}=7:5$

c.

To determine

To find: The area ratio of whole region PST and shaded region PQR .

Answer to Problem 26RP

The area ratio is $4:1$ .

Explanation of Solution

Given information:

Side ST = 10,

Side PQ = QS,

Side PR = RT.

Formula used:

The below Midline theorems is used:

The midline theorem claims that cutting along the midline of a triangle creates a segment that is parallel to the base and half as long.

The below similar figures theorem is used:

If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of ratio of their corresponding sides. This proves that the ratio of the area of two similar triangles is proportional to the squares of the corresponding sides of both the triangles.

Calculation:

  

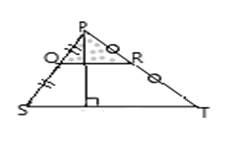
Using Midline Theorem, the base of the shaded triangle is parallel to and is half of the base of the whole triangle.

Using Reflexive angle and two angles proven congruent by parallel lines implies corresponding angles are congruent.

The shaded triangle is similar to whole triangle by AA similarity rule.

By Similar Figures Theorem, we get

Side ST = 10

  $QR=\frac{ST}{2}=\frac{10}{2}=5$

  $\frac{A_{WholeTriangle}}{A_{ShadedTriangle}}={\left(\frac{s_1}{s_2}\right)}^2={\left(\frac{ST}{QR}\right)}^2={\left(\frac{10}{5}\right)}^2=\frac{100}{25}=4:1$