Chapter 11.2, Problem 33PSC

a.

To determine

To show the sum ofarea of triangleAPD and triangle BPC is equal to sum of area of triangle APB and triangle PCD.

Explanation of Solution

Given:

P is any point interior of rectangle ABCD.

Formula Used:

  $\begin{array}{l}Areaofrectangle=b\ast h\\ b=Base,\\ h=Height\end{array}$

  $\begin{array}{l}Areaoftriangle=\frac{1}{2}\ast b\ast h\\ b=Base,\\ h=Height\end{array}$

Proof:

  

In rectangle, opposite sides are equal.

  $\begin{array}{l}AD=BC,\\ AB=DC\end{array}$

  $\begin{array}{l}{A}_{\Delta APD}+A_{\Delta BPC}=(\frac{1}{2}*h_1*AD)+(\frac{1}{2}*h_2*BC)\\ AD=BC\\ =\frac{1}{2}*2AD*(h_1+h_2)\\ =AD*h\\ =\text{Area of}\text{rectangle}ABCD\end{array}$

  $\begin{array}{l}{A}_{\Delta APB}+A_{\Delta PCD}=(\frac{1}{2}*h_3*AB)+(\frac{1}{2}*h_4*DC)\\ AB=DC\\ =\frac{1}{2}*(h_3+h_4)\\ =\frac{1}{2}*h*2AB\\ =AB*h\\ =Areaofrec\tan gleABCD\end{array}$

  $\therefore A_{\Delta APD}+A_{\Delta BPC}=A_{\Delta APB}+A_{\Delta PCD}$

b.

To determine

To state whether equation formed by sum of area of triangle APD and triangle BPC is equal to sum of area of triangle APB and triangle PCDfor a parallelogram ABCD is valid.

Answer to Problem 33PSC

Yes, the equation formed by sum of area of triangle APD and triangle BPC is equal to sum of area of triangle APB and triangle PCDfor a parallelogram ABCD is valid.

Explanation of Solution

Given:

P is any point interior of parallelogram ABCD.

Formula Used:

  $\begin{array}{l}Areaofrectangle=b\ast h\\ b=Base,\\ h=Height\end{array}$

  $\begin{array}{l}Areaoftriangle=\frac{1}{2}\ast b\ast h\\ b=Base,\\ h=Height\end{array}$

Calculation:

  

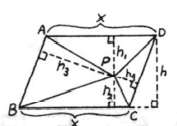
In parallelogram, opposite sides are congruent.

  $\begin{array}{l}AD=BC,\\ AB=DC\end{array}$

  $\begin{array}{l}{A}_{\Delta APD}+A_{\Delta BPC}=(\frac{1}{2}*h_1*AD)+(\frac{1}{2}*h_2*BC)\\ AD=BC\\ =\frac{1}{2}*2AD*(h_1+h_2)\\ =AD*h\\ =\text{Area of parallelogram}\end{array}$

  $\begin{array}{l}{A}_{\Delta APB}+A_{\Delta PCD}=(\frac{1}{2}*h_3*AB)+(\frac{1}{2}*h_4*DC)\\ AB=DC\\ =\frac{1}{2}*(h_3+h_4)\\ =\frac{1}{2}*h*2AB\\ =AB*h\\ =\text{Area of parallelogram}\end{array}$

  $\therefore A_{\Delta APD}+A_{\Delta BPC}=A_{\Delta APB}+A_{\Delta PCD}$

c.

To determine

To check whether equation formed by the sum of area of triangle APD and triangle BPC is equal to sum of area of triangle APB and triangle PCDfor a trapezoid ABCD is correct.

Answer to Problem 33PSC

No, the equation formed by sum of area of triangle APD and triangle BPC is equal to sum of area of triangle APB and triangle PCDfor a trapezoid ABCD is not correct.

Explanation of Solution

Given:

P is any point interior of trapezoid ABCD.

Formula Used:

  $\begin{array}{l}Areaofrectangle=b\ast h\\ b=Base,\\ h=Height\end{array}$

  $\begin{array}{l}Areaoftriangle=\frac{1}{2}\ast b\ast h\\ b=Base,\\ h=Height\end{array}$

Calculation:

  

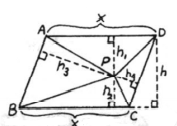
In trapezoid, opposite sides are not necessarily congruent.

  $\begin{array}{l}AD\ne BC,\\ AB\ne DC\end{array}$

Also, altitude to nonparallel sides are non collinear.

  $\begin{array}{l}{A}_{\Delta APD}+A_{\Delta BPC}=(\frac{1}{2}*h_1*AD)+(\frac{1}{2}*h_2*BC)\\ =x\text{ say}\end{array}$

  $\begin{array}{l}{A}_{\Delta APB}+A_{\Delta PCD}=(\frac{1}{2}*h_3*AB)+(\frac{1}{2}*h_4*DC)\\ =y\text{say}\end{array}$

  $\begin{array}{l}x\ne y\\ \therefore A_{\Delta APD}+A_{\Delta BPC}\ne A_{\Delta APB}+A_{\Delta PCD}\end{array}$