Chapter 11.3, Problem 8PSB

a.

To determine

To calculate: Total area of the given figure with upper base $7$ and measure of an angle which is ${60}^{\circ }$ .

Answer to Problem 8PSB

The total area of the given figure is $30\sqrt{3}$ ${\text{unit}}^{\text{2}}$

Explanation of Solution

Given:

The length of the upper base ( a )= $7$

The measure of an angle is ${60}^{\circ }$

Concept used:

Here, we are using the formula

Area of trapezoid = $\frac{1}{2}\left(a+b\right)\times h$

(Where, “ a ” is upper base, “ b ” is lower base and “ h” is height)

Calculation:

  

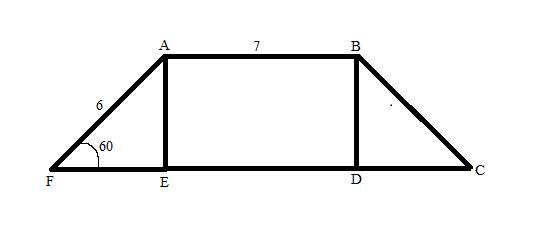
Here, we know that Sin $\theta =\frac{P}{H}$

In $\Delta AFE$

→Sin ${60}^{\circ }=\frac{P}{H}$ (here, “ P ” is perpendicular and “ H ” is hypotenuse)

  $\frac{\sqrt{3}}{2}=\frac{P}{AF}$

  $\frac{\sqrt{3}}{2}=\frac{P}{6}$

  $P=3\sqrt{3}$

Similarly, Tan ${60}^{\circ }=\frac{P}{B}$ (here, “ P ” is perpendicular and “ B ” is base)

  $\sqrt{3}=\frac{3\sqrt{3}}{FE}$

Where FE is base

  $FE"B"=3$

Now, Area of trapezoid = $\frac{1}{2}\left(a+b\right)\times h$ (here, “ a ” is upper base, “ b ” is lower base and “ h” is height)

→ $\frac{1}{2}\left(7+3\right)\times 3\sqrt{3}$

→ $30\sqrt{3}$

Conclusion: Hence, the total area of the given figure is $30\sqrt{3}$ ${\text{unit}}^{\text{2}}$

b.

To determine

To calculate:Total area of the given figure with the length of upper base which is $10$ and median is $16$

Answer to Problem 8PSB

The total area of the given figure is $52+10\sqrt{11}$ ${\text{unit}}^{\text{2}}$

Explanation of Solution

Given: Lengths of upper base (a ) = $10$

lower base( b)= $4$

median ( m )= $16$

Formula used:

Here, the formula is

Area of trapezoid = $\frac{1}{2}\left(a+b\right)\times h$

(here, “ a ” is upper base, “ b ” is lower base and “ h” is height)

Calculation:

  

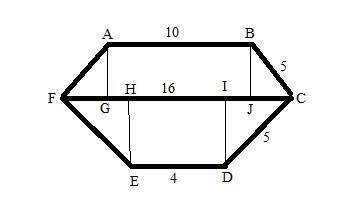
Here, let area of trapezoid ABFC be $A_1$

Area of trapezoid = $\frac{1}{2}\left(a+b\right)\times h$

(here, “ a ” is upper base, “ b ” is lower base and “ h” is height)

Firstly, we need to find the height of trapezoid ABFC

In $\Delta JBC$

  ${\left(hypotenuse\right)}^2={\left(perpendicular\right)}^2+{\left(base\right)}^2$

  ${\left(BC\right)}^2={\left(BJ\right)}^2+{\left(JC\right)}^2$

  ${\left(5\right)}^2={\left(BJ\right)}^2+{\left(3\right)}^2$

  $BJ=\sqrt{25-9}=4$

So, the height ( h ) of trapezoid ABFC is $4$

Therefore, Area of the trapezoid ABFCwould be

  $A_1=\frac{1}{2}\left(AB+FC\right)\times 4$

  $A_1=\frac{1}{2}\left(10+16\right)\times 4$

  $A_1=52$

Now, let area of trapezoid FCED be $A_2$

Area of trapezoid = $\frac{1}{2}\left(a+b\right)\times h$

(here, “ a ” is upper base, “ b ” is lower base and “ h” is height)

Firstly, we need to find the height of trapezoid FCED

In $\Delta DIC$

  ${\left(hypotenuse\right)}^2={\left(perpendicular\right)}^2+{\left(base\right)}^2$

  ${\left(DC\right)}^2={\left(ID\right)}^2+{\left(IC\right)}^2$

  ${\left(5\right)}^2={\left(ID\right)}^2+{\left(6\right)}^2$

  $ID=\sqrt{36-25}=\sqrt{11}$

So, the height ( h ) of trapezoid FCED is $\sqrt{11}$

Therefore, Area of the trapezoid FCEDwould be

  $A_2=\frac{1}{2}\left(16+4\right)\times \sqrt{11}$

  $A_2=10\sqrt{11}$

So, Total area = $A_1+A_2$

→ $52+10\sqrt{11}$

Conclusion: Hence, the total area of the given figure is $52+10\sqrt{11}$ ${\text{unit}}^{\text{2}}$