
Concept explainers
The motion of a vibrating particle is defined by the position
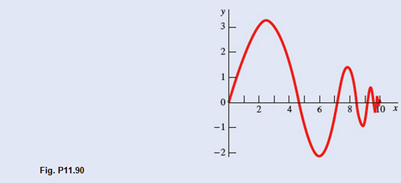
(a)
The velocity and acceleration when t=0.
Answer to Problem 11.90P
Explanation of Solution
Given information:
The motion of a vibrating particle is defined by the position vector,
Where, (r) in millimetres and (t) is in seconds.
We can obtain the velocity (v) at any time (t) by differentiating (r) with respect to (t),
Since,
The acceleration (a) can be obtained by differentiating again the above equation with respect to (t),
When t=0,
Velocity,
And, acceleration,
(b)
The velocity and acceleration when t=0.5.
Answer to Problem 11.90P
Explanation of Solution
Given information:
The motion of a vibrating particle is defined by the position vector,
Where, (r) in millimetres and (t) is in seconds.
We can obtain the velocity (v) at any time (t) by differentiating (r) with respect to (t),
Since,
The acceleration (a) can be obtained by differentiating again the above equation with respect to (t),
When t=0.5,
Velocity,
And, acceleration,
Want to see more full solutions like this?
Chapter 11 Solutions
Vector Mechanics for Engineers: Dynamics
- A car P travels along a straight road with a constant speed v = 64 mi/hr. At the instant when the angle 0 = 60°, determine the values of r in ft/sec and 8 in deg/sec. Assume = 113! Answers: r = 1 0 = F MI x חומון V ft/sec deg/secarrow_forwardA body moves along a linear path and its rate of change of velocity varies with time and is written as a=2-3t, where t is the time in second. After 5 second, from start of observation its velocity is determined to be 20 m/s. After 10 second from start of observation, the body is at 85 m far from the origin. Determine the following:a. Rate of change of velocity and velocity at the start of motion.b. Distance from the origin at the start of observationc. Time after start of observation in which the velocity becomes zero.arrow_forwardquestionarrow_forward
- The rectangular coordinates of a particle which moves with curvilinear motion are given by x= 10.00t+1.00t² - 0.55+³ and y = 6.32 + 10.10t - 2.22t², where x and y are in millimeters and the time t is in seconds, beginning from t = 0. Determine the velocity v and acceleration a of the particle when t = 8 s. Also, determine the first time that the velocity of the particle makes an angle of 18° with the positive x-axis. Answers: V = a = (i t = tel it i i+i S j) mm/s j) mm/s²arrow_forwardThe rectangular coordinates of a particle which moves with curvilinear motion are given by x = 10.75t +2.25t² - 0.45t³ and y = 6.90 + 17.43t - 2.62t², where x and y are in millimeters and the time t is in seconds, beginning from t = 0. Determine the velocity v and acceleration a of the particle when t = 8 s. Also, determine the first time that the velocity of the particle makes an angle of 30° with the positive x-axis. Answers: V = a = 17.1 10.75 i + i 5.24 i+ i 17.43 j) mm/s j) mm/s²arrow_forwardThe motion of a particle is given by the relation a = 6t, where t is in sec and a in m/s2. If s = 8m and v = 4m/s when t = 1s, determine the s – a equation. a. s = (s/a)1/3 + a/6 + 6 b. s = (a/6)3 + a/6 – 1 c. s = (s/a)3 – a/6 + 6 d. none e. s = (a/6)3 + a/6 + 6arrow_forward
- At time t = 0, the position vector of a particle moving in the x-y plane is r = 4.78i m. By time t = 0.019 s, its position vector has become (4.96i + 0.52j) m. Determine the magnitude Vay of its average velocity during this interval and the angle e made by the average velocity with the positive x- axis. Answers: Vav Ꮎ = = i i m/sarrow_forwardhelp what is the correct answerarrow_forwardSubject :- Mechanical Engineeringarrow_forward
- Dynamics of Rigid Bodies - Mechanical Engineering The velocity of a particle moving in the x-y plane is given by (6.91i + 7.17j) m/s at time t = 5.61 s. Its average acceleration during the next 0.017 s is (2.7i + 4.3j) m/s^2. Determine the velocity v of the particle at t = 5.627 s and the angle O between the average-acceleration vector and the velocity vector at t = 5.627 s. Subject: Mechanical Engineeringarrow_forwardA particle in an experimental apparatus has a velocity given by v = k√s, where v is in millimeters per second, the position s is millimeters, and the constant k = 0.36 mm ¹/25-¹1. If the particle has a velocity vo = 6 mm/s at t = 0, determine the particle position, velocity, and acceleration as functions of time. To check your work, evalutate the time t, the positions, and the acceleration a of the particle when the velocity reaches 35 mm/s. Answers: t = i S= i a = i S mm mm/s²arrow_forward• 1. A particle position given by s(t) = 4 t2 - 32 t +36 with s in meters and t in seconds. At what position does the particle come to a # 1 %3D momentary stop to reverse its motion? par • 2. A particle moves in a straight line such that for a short time its velocity is defined by V = ( 4t3 + 3t2 seconds. Determine its position and acceleration when t = 3 s; 2t) ft/s, where t is in %3D %3D he when t = 0, S = 0 %3D e pa he particle for wertical disola reach the ground tance that the paticle travel haght of the paratle, he t lury paricle when the bonzonl distence i 70 m dislmce whn the hayht uf the paricle is %23arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





