Chapter 11.3, Problem 11.65P

To determine

(a)

The construction of $a-t$ and $x-t$ curves for $0\le t\le 40\text{s}$.

The maximum value of the position coordinate of the particle.

Answer to Problem 11.65P

The curves for $a-t$ graph is drawn in Figure 1 and the curve of $x-t$ graph is given in Figure 2.

The maximum value of position coordinate of the particle is $162\text{ft}$.

Explanation of Solution

Given:

The particle starts from origin with an initial displacement of $x_0=-48\text{ft}$.

Concept used:

The particle moves with constant velocity of $6\text{ft/s}$ for $0\le t\le 10\text{s}$, then with constant positive acceleration for $10<t\le 18\text{s}$ and velocity of $18\text{ft/s}$ at $18\text{s}$, then with constant negative acceleration for $18<t\le 30\text{s}$ and velocity $0\text{ft/s}$ at $24\text{s}$ and $-18\text{ft/s}$ at $30\text{s}$. After that it moves with zero acceleration indefinitely.

Change in the displacement for the given $v-t$ plot in the interval is the area under the $v-t$ graph for that duration.

$x_f-x_i=\text{area under the }v-t\text{curve}$ ...... (1)

Here $x_f$ is the final displacement and $x_i$ is the initial displacement.

Write the formula for acceleration as a time derivative of velocity.

$a=\frac{dv}{dt}$ ...... (2)

Here $a$ is the acceleration and $\frac{dv}{dt}$ is time derivative of velocity.

For the duration of time $0\le t\le 10\text{s}$, the velocity is constant. This means $\frac{dv}{dt}$ is zero. Therefore, for this interval, the acceleration is zero.

From the given graph for the time interval $10\le t\le 18\text{s}$ the velocity increases linearly with time. This means the value of $\frac{dv}{dt}$ is constant and hence, the acceleration is constant.

Write the formula to calculate, the acceleration from the data given in the graph.

$a=\frac{v_2-v_1}{t_2-t_1}$ ...... (3)

Here $v_2$ is final velocity and $v_1$ is initial velocity. The value of $t_2-t_1$ is change in time.

Calculation:

For the duration of $0\le t\le 10\text{s}$ the acceleration is calculated as follows:

Substitute $6\text{ft/s}$ for $v_2$, $6\text{ft/s}$ for $v_1$, $0\text{s}$ for $t_1$ and $10\text{s}$ for $t_2$ and in equation (3).

$\begin{array}{c}a=\frac{v_2-v_1}{t_2-t_1}\\ =\frac{6-6}{10-0}\\ =0{\text{ft/s}}^2\end{array}$

The displacement forthis interval is calculated as follows:

Substitute $-48\text{ft}$ for initial displacement $x_1$ and the area under the curve for an interval $0\le t\le 10\text{s}$ in equation (1).

$\begin{array}{c}{x}_2-\left(-48\right)=\left(6\right)\left(10\right)\\ x_2=60-48\\ =12\text{ft}\end{array}$

Substitute $18\text{ft/s}$ for $v_2$, $6\text{ft/s}$ for $v_1$, $10\text{s}$ for $t_1$ and $18\text{s}$ for $t_2$ and in equation (3).

$\begin{array}{c}a=\frac{18-6}{18-10}\\ =1.5{\text{ft/s}}^2\end{array}$

Substitute $12\text{ft}$ for initial displacement $x_2$ and the area under the curve forinterval $10<t\le 18\text{s}$ in equation (1).

$\begin{array}{c}{x}_3-\left(12\right)=\frac{1}{2}\left(6+18\right)\left(18-10\right)\\ x_3=12+\left(12\right)\left(8\right)\\ =108\text{ft}\end{array}$

For the time duration $18<t\le 24\text{s}$, the acceleration is calculated as:

Substitute $0\text{ft/s}$ for $v_2$, $18\text{ft/s}$ for $v_1$, $18\text{s}$ for $t_1$ and $24\text{s}$ for $t_2$ and in equation (3).

$\begin{array}{c}a=\frac{0-\left(18\right)}{24-18}\\ =\frac{-18}{6}\\ =-3{\text{ft/s}}^2\end{array}$

The displacement for this time interval is calculated as follows:

Substitute $108\text{ft}$ for initial displacement $x_3$ and the area under the curve for an interval $18<t\le 24\text{s}$ in equation (1).

$\begin{array}{c}{x}_4-\left(108\right)=\frac{1}{2}\left(18-0\right)\left(24-18\right)\\ x_4=108+\left(9\right)\left(6\right)\\ =162\text{ft}\end{array}$

For the duration $24<t\le 30\text{s}$, the acceleration is calculated as:

Substitute $-18\text{ft/s}$ for $v_2$, $0\text{ft/s}$ for $v_1$, $24\text{s}$ for $t_1$ and $30\text{s}$ for $t_2$ and in equation (3).

$\begin{array}{c}a=\frac{-18-0}{30-24}\\ =\frac{-18}{6}\\ =-3{\text{ft/s}}^2\end{array}$

The displacement for this interval is calculated as follows:

Substitute $162\text{ft}$ for initial displacement $x_4$ and the area under the curve for an interval $24<t\le 30\text{s}$ in equation (1).

$\begin{array}{c}{x}_5-\left(162\right)=\frac{1}{2}\left(-18-0\right)\left(30-24\right)\\ x_5=162-\left(9\right)\left(6\right)\\ =108\text{ft}\end{array}$

For the time duration $30<t\le 40\text{s,}$ the acceleration is calculated as:

Substitute $-18\text{ft/s}$ for $v_2$, $-18\text{ft/s}$ for $v_1$, $30\text{s}$ for $t_1$ and $40\text{s}$ for $t_2$ and in equation (3).

$\begin{array}{c}a=\frac{-18-\left(-18\right)}{40-30}\\ =\frac{0}{10}\\ =0{\text{ft/s}}^2\end{array}$

The displacement for this interval is calculated as follows:

Substitute $108\text{ft}$ for initial displacement $x_5$ and the area under the curve for an interval $30<t\le 40\text{s}$ in equation (1).

$\begin{array}{c}{x}_6-\left(108\right)=\left(-18-0\right)\left(40-30\right)\\ x_6=108+\left(-18\right)\left(10\right)\\ =-72\text{ft}\end{array}$

The $a-t$ plotwith the help of acceleration values calculated at different intervalsis drawn in Figure 1.

The $x-t$ plot with the help of displacement values calculated at different intervals is drawn in Figure 2.

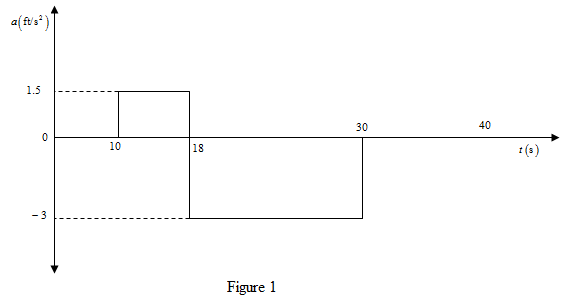
Therefore, from the graph, the maximum value of displaced particle is $162\text{ft}$.

Conclusion:

The curves for $a-t$ graph is drawn in Figure 1 and the curve of $x-t$ graph is given in Figure 2 and the maximum value of position coordinate of the particle is $162\text{ft}$.

To determine

(b)

The values of $t$ at a distance of $108\text{ft}$ from the origin.

Answer to Problem 11.65P

The values of $t$ at a distance of $108\text{ft}$ from the origin are $18\text{s}$ and $30\text{s}$.

Explanation of Solution

The $x-t$ plot is calculated by the values of displacements at various points of time by calculating area under the $v-t$ plot and by evaluating the increase and decrease of the velocity, the slopes of $x-t$ plot are interpreted.

From the $x-t$ plot drawn in the Figure 2, it can be seen that the curve increases from $t=18\text{s}$ to $t=24\text{s}$ and decreases from $t=24\text{s}$ to $t=30\text{s}$. During these intervals, the displacement of $108\text{ft}$ is achieved at two points of time. One, at $t=18\text{s}$ and other at $t=30\text{s}$.

Conclusion:

Thus, the values of $t$ at a distance of $108\text{ft}$ from the origin are $18\text{s}$ and $30\text{s}$.