Chapter 4.5, Problem 97AYU

Mixed Practice In Problems $93-104$, grapheach polynomial function.

$f\left(x\right)=4x^4+7x^2-2$

To determine

To graph: The polynomial function $f\left(x\right)=4x^4+7x^2-2$

Explanation of Solution

Given Information:

The polynomial function $f\left(x\right)=4x^4+7x^2-2$

Graph:

The steps of graph of the polynomial function as follows:

Step 1: First, find the end behavior of the graph of the function $f\left(x\right)=4x^4+7x^2-2$.

Here, the degree of the polynomial function $f\left(x\right)$ is 4

The graph of the function $f\left(x\right)=4x^4+7x^2-2$ behaves like $y=x^4$ for large values of $\left|x\right|$

Step 2: Find $x$ and $y-$ intercepts of the graph of the function.

For the $y-$ intercept, substitute $x=0$ in the function $f\left(x\right)=4x^4+7x^2-2$

$f\left(0\right)=4{\left(0\right)}^4+7{\left(0\right)}^2-2=-2$.

Thus, the $y-$ intercept of the polynomial function is $-2$.

For the $x-$ intercept, that is, zeros of the function, use the Rational Zeros Theorem.

$f\left(x\right)=4x^4+7x^2-2=0$

Since there is 1 variation in the sign of the non-zero coefficients of $f\left(x\right)$, hence, by using the Descartes’ Rule of Signs, there is 1 positive real zero or 0 positive real zero.

$f\left(-x\right)=4{\left(-x\right)}^4+7{\left(-x\right)}^2-2$

$\Rightarrow f\left(-x\right)=4x^4+7x^2-2$

There is 1 variation in the sign of the non-zero coefficients of $f\left(-x\right)$, hence, by using Descartes’ Rule of Signs, there is one negative real zero or 0 positive real zero.

By using the Rational Zero Theorem, all possible rational zeroes are of the form $x=\frac{p}{q}$, where $p$ means all factors of the constant term in the polynomial and $q$ means all factors of the leading term of the polynomial.

In the polynomial $f\left(x\right)=4x^4+7x^2-2$, the constant term is 2 and the leading term is 4

Factors of the constant term $p=2$ are $\pm 1,\pm 2$

Factors of the leading term $q=4$ are $\pm 1,\pm 2,\pm 4$.

Therefore, all possible rational zeros are:

$\frac{p}{q}:$ $\pm \frac{1}{1},\pm \frac{1}{2},\pm \frac{1}{4},\pm \frac{2}{1},\pm \frac{2}{2},\pm \frac{2}{4}$.

Simplifies to,

$\frac{p}{q}:\pm \frac{1}{2},\pm \frac{1}{4},\pm 1,\pm 2$.

As there are $1\text{or}0$ positive and $1\text{or}0$ negative real zero, all the potential rational zeros of the polynomial function $f\left(x\right)=4x^4+7x^2-2$ are $x=\pm \frac{1}{2},\pm \frac{1}{4},\pm 1,\pm 2$ $$

Now, test $x=\frac{1}{2}$ using the synthetic division.

$\begin{array}{l}\frac{1}{2}\overline{)4070-2}\\ \underset{\_}{2142}\\ 42840\end{array}$

Here, since the remainder is 0, $x=\frac{1}{2}$ is a zero of $f$ and $\left(x-\frac{1}{2}\right)$ is a factor of $f$.

To write the factors of $f$, use the entries in the bottom row of the above synthetic division.

$f\left(x\right)=4x^4+7x^2-2=\left(x-\frac{1}{2}\right)\left(4x^3+2x^2+8x+4\right)$

Here, $f\left(x\right)=4x^3+2x^2+8x+4$ is called a depressed equation.

Any solution to this depressed equation is also a zero of $f$, so now find zeros of this depressed equation.

The depressed equation $f\left(x\right)=4x^3+2x^2+8x+4=0$ can be factored as follows:

$4x^3+2x^2+8x+4=2x^2\left(2x+1\right)+4\left(2x+1\right)=0$

$\Rightarrow \left(2x^2+4\right)\left(2x+1\right)=0$

$\Rightarrow \left(2x^2+4\right)=0$ and $2x+1=0$

$\Rightarrow x^2=-\frac{4}{2}=-2$ and $x=-\frac{1}{2}$

$x^2=-2$ does not give a real solution

Thus, the real zeros of the polynomial function $f\left(x\right)=4x^4+7x^2-2$ is $x=\frac{1}{2},-\frac{1}{2}$.

Step 3: The maximum number of turning points on the graph of the function $f\left(x\right)=4x^4+7x^2-2$ are $4-1=3$, since the polynomial function has degree 4.

The polynomial function $f\left(x\right)=4x^4+7x^2-2$ has degree 4 and two real zeroes at $x=-\frac{1}{2}$ and $x=\frac{1}{2}$; hence, the graph crosses the $x$-axis at $x=-\frac{1}{2}$ and $x=\frac{1}{2}$

Step 4: Now, use the information obtained in step 1 to 3 to draw the graph of the function $f\left(x\right)$ as follows:

Now, find additional points on the graph.

For $x=-1$, the value of $f\left(x\right)$, at $x=-1$, is $f\left(-1\right)=4{\left(-1\right)}^4+7{\left(-1\right)}^2-2=9$.

For $x=1$, the value of $f\left(x\right)$, at $x=1$, is $f\left(1\right)=4{\left(1\right)}^4+7{\left(1\right)}^2-2=9$.

Now, plot all these coordinates $\left(-1,9\right)$ and $\left(1,9\right)$ on the graph and join them.

So, the graph of the function is obtained as follows:

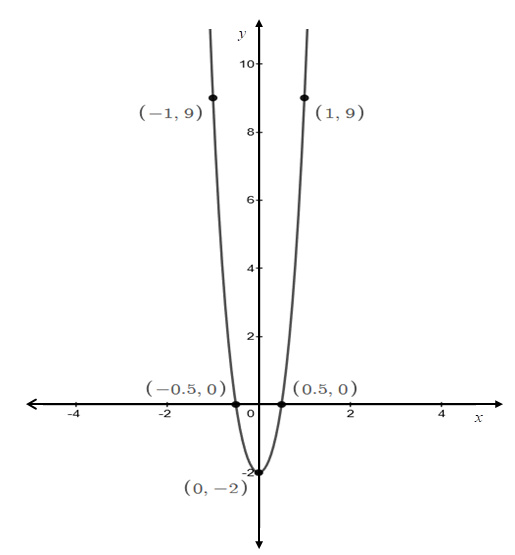
Interpretation:

The graph represents the polynomial function $f\left(x\right)=4x^4+7x^2-2$.