
To discuss: the given rational function.
Answer to Problem 26RE
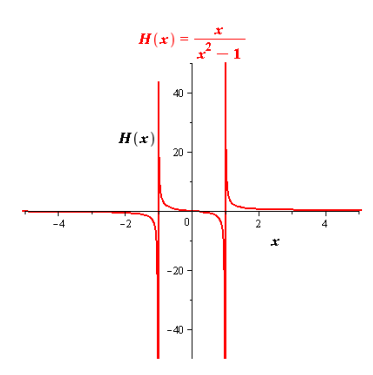
Explanation of Solution
Given:
Explanations:
Let us consider the following rational function,
analyze the graph of the given function.
For this follow the following steps:
Step
Determination the domain of the function. Domain of a function is defined as the set of values of
So, let us first find the values of
So, at
Therefore, the domain of the function is
Step
Write
Here, since there is no common factor between the numerator and the denominator,
Step
Next, approximate
So,
Since there is only one zero of the numerator, there is only one
Also, since
So, the
Step
Determine whether the function is odd, even or neither.
A function is even if,
Also, a function is odd if,
So, let us first find the values of
Therefore, the function is not odd.
So, the graph is symmetric about origin.
Step
Find the vertical asymptotes.
The vertical asymptotes of a rational function are located at the real zeros of the denominator.
As found above, the real zero of the denominator are
So, the vertical asymptote of the function lies at
Step
Find the horizontal or oblique asymptotes. Also, locate the points where the asymptote intersects the graph.
Here, the degree of the numerator is smaller than the denominator. Therefore, this is a proper rational function. So,
Therefore, the horizontal asymptote of the function lies at
To determine where the graph intersects the horizontal asymptote, solve
So,
So, the graph intersects the horizontal asymptote at
Step
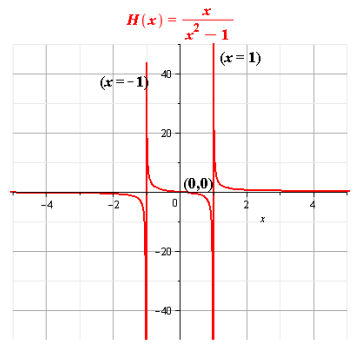
Graph
Step
Complete the graph using all the above information.
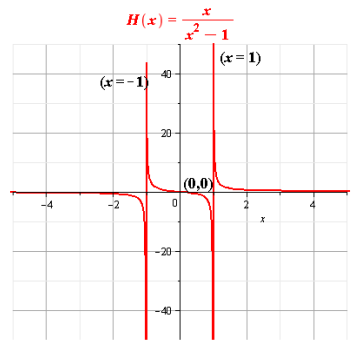
Conclusion:
Therefore,the given rational function is analyzed.
Chapter 4 Solutions
Precalculus
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Thinking Mathematically (6th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics
Elementary Statistics: Picturing the World (7th Edition)
Algebra and Trigonometry (6th Edition)
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. 2 f'(x) N -5 -4 3-2-1 -1 -2 -3 -4 12 3 4 5 -x Local minima at x Local maxima at xarrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. -5-4-32 4- 3 2 1 -2 -3 +x 2 3 4 5arrow_forwardThe graph of f' is below. Use it to determine where the inflection points are and the intervals where f is concave up and concave down. If there are multiple inflection points, separate with a comma. 6 5 4 3 2 1 f'(x) +x -6-5-4-3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6+ Inflection point(s) at x = Concave up: Concave down:arrow_forward
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. f'(x) 4- -5-4-3-8-1 3 2 1 x 1 2 3 4 5 -1 -2 -3 -4 Local minima at a Local maxima at =arrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. f'(xx) 4- -5 -3 -2 3 2 1 1 2 3 4 5 Cit +x 7 2arrow_forwardPlease focus on problem ii.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





