Chapter 4.1, Problem 99AYU

To determine

To analyze: the given polynomial function

Answer to Problem 99AYU

Figure 1(a):

  

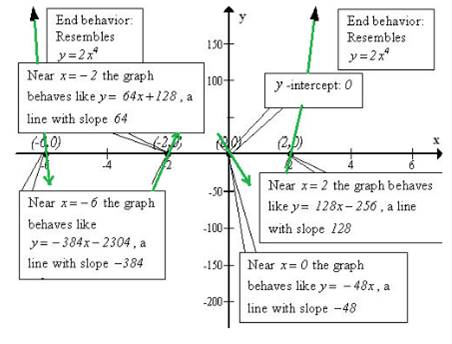
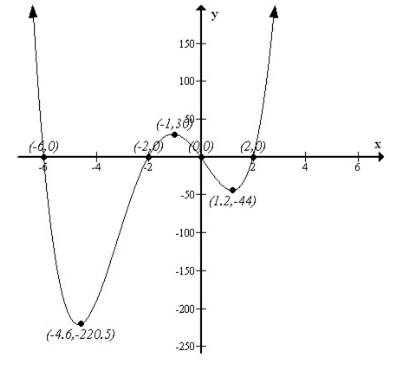
Figure 1(b):

  

Explanation of Solution

Given:

  $f\left(x\right)=2x^4+12x^3-8x^2-48x$

Calculation:

Let us consider the function $f\left(x\right)=2x^4+12x^3-8x^2-48x$

This polynomial function $f\left(x\right)$ can be factored as

  $\begin{array}{l}\begin{array}{l}f\left(x\right)=2x^4+12x^3-8x^2-48x\\ =2x\left(x^3+6x^2-4x-24\right)\end{array}\hfill \\ =2x\left\{x^2\left(x+6\right)-4\left(x+6\right)\right\}\hfill \\ \begin{array}{l}=2x\left(x^2-4\right)\left(x+6\right)\\ =2x\left(x-2\right)\left(x+2\right)\left(x+6\right)\end{array}\hfill \end{array}$

Step1: Determine the end behavior of the graph of the function

Expand the polynomial to write it in the form

  $\begin{array}{l}\begin{array}{l}f\left(x\right)=\text{ 2}x\left(x-2\right)\left(x+2\right)\left(x+6\right)\\ =2x\left(x^2-4\right)\left(x+6\right)\text{ since }\left(x-a\right)\left(x+a\right)=x^2-a^2\end{array}\hfill \\ =\left(2x^3-8x\right)\left(x+6\right)\hfill \\ \begin{array}{l}=2x^4-8x^2+12x^3-48x\\ =2x^4+12x^3-8x^2-48x\end{array}\hfill \end{array}$

The polynomial function f is of degree 4. The graph of f behaves like $y=2x^4$ for large values of $\left|x\right|$ .

Step2: find the x -and y -intercepts of the graph of the function

Substitute $x=0$ in the given function. Get the result 0.

The y -intercept is $f\left(0\right)=0$ .

To find the x -intercepts, solve $f\left(x\right)=0$ ,

  $\text{2}x\left(x-2\right)\left(x+2\right)\left(x+6\right)=0$

If and only if any of the factors is zero.

So, $x=0,2,-2,-6$ are the x -intercepts of the given polynomial $f\left(x\right)=2x^4+12x^3-8x^2-48x$ .

Step3: Determine the zeros of the function and their multiplicity. Use this information to determine whether the graph crosses or touches the x -axis at each x -intercept.

The zeros or roots of fare obtained from $\text{2}x\left(x-2\right)\left(x+2\right)\left(x+6\right)=0$

That is $x=-6,-2,0,2$ .

The root-6is a zero of multiplicity 1, so the graph off crosses the x -axis at $x=-6$ only once.

The root -2 is a zero of multiplicity1. So the graph of f crosses thex -axis at 2^nd time.

The root 0 is a zero of multiplicity 1 and the curve crosses the x -axis for the 3^rd time.

The zero 2 is a zero of multiplicity 1 and so, the curve crosses x -axis for the 4^th time.

Therefore there are 3 turning points to the curve $f\left(x\right)=2x^4+12x^3-8x^2-48x$

Step 4: Determine the maximum number of turning points on the graph of the function.

While the polynomial function $f\left(x\right)=2x^4+12x^3-8x^2-48x$ is of degree 4, the graph of the function will have at most $4-1=3$ points.

Step5: Determine the behavior of the graph of f near each x -intercept.

Thex -intercepts with the function $f\left(x\right)=2x^4+12x^3-8x^2-48x$ are - 6,-2, 0, and 2.

So, the behavior of the function near -6 is

  $\begin{array}{l}f\left(x\right)=2x\left(x-2\right)\left(x+2\right)\left(x+6\right)\\ \approx 2\left(-6\right)\left(-6-2\right)\left(-6+2\right)\left(x+6\right)\\ \approx -384\left(x+6\right)\\ \approx -384x-2304\end{array}$

This is a straight line with a negative slope -384.

The behavior of f at -2 is:

  $\begin{array}{l}f\left(x\right)=2x\left(x-2\right)\left(x+2\right)\left(x+6\right)\\ \approx 2\left(-2\right)\left(-2-2\right)\left(x+2\right)\left(-2+6\right)\\ \approx 64\left(x+2\right)\\ \approx 64x+128\end{array}$

This is a straight line with a positive slope 64.

The behavior of f at 0 is:

  $\begin{array}{l}f\left(x\right)=2x\left(x-2\right)\left(x+2\right)\left(x+6\right)\\ \approx 2x\left(0-2\right)\left(0+2\right)\left(2+6\right)\\ \approx -48x\end{array}$

This is a straight line with a negative slope -48.

The behavior of f at 2 is:

  $\begin{array}{l}f\left(x\right)=2x\left(x-2\right)\left(x+2\right)\left(x+6\right)\\ \approx 2\left(2\right)\left(x-2\right)\left(2+2\right)\left(2+6\right)\\ \approx 128\left(x-2\right)\\ \approx 128x-256\end{array}$

This is a straight line with a positive slope 128.

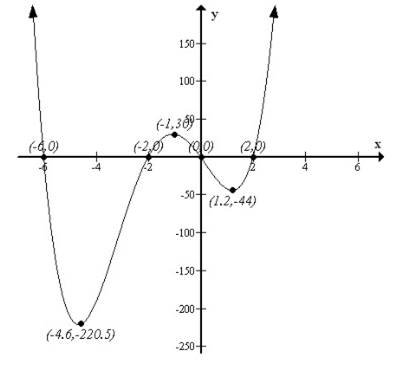
Step 6: Put all the information from Steps 1 through 5 together to obtain the graph of f Figure 1(a) illustrates the information obtained from Steps 1 through 5. Evaluatef at -4.6, -1, 1.2 to help establish the scale on the y -axis.

The graph of f is given in Figure 1(b).

Figure 1(a):

  

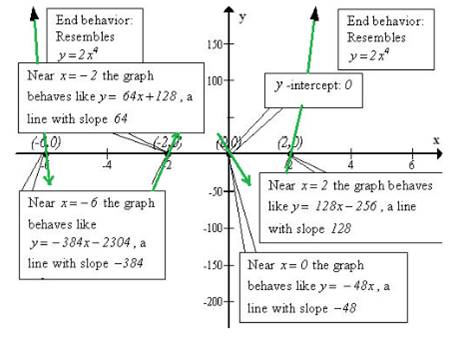
Figure 1(b):

  

Conclusion:

Therefore, the polynomial function $f\left(x\right)=2x^4+12x^3-8x^2-48x$ is analysed with graph.