Chapter 4.3, Problem 56AYU

(a)

To determine

To find: the amount of material required to make the drum

Answer to Problem 56AYU

The amount of material required to make the drum is $A=\frac{200}{r}+2\pi r^2$.

Explanation of Solution

Given:

Volume = 100 cubic feet

Calculation:

Find the amount of the material required to make the right circular cylinder as a function of its radius

For this, find the volume of the right circular cylinder

The volume of a right circular cone is

  $V=\pi r^{2}h$

Here r denotes the radius of the cylinder.

And h denotes the height of the cylinder.

Now

  $\begin{array}{l}\pi r^{2}h=100\\ h=\frac{100}{\pi r^2}\end{array}$

Now write its total surface area as a function of time

  $\begin{array}{l}A=2\pi r^2+2\pi rh\hfill \\ \begin{array}{l}=2\pi r^2+2\pi \times \frac{100}{\pi r^2}\\ A=\frac{200}{r}+2\pi r^2\end{array}\hfill \end{array}$

Conclusion:

Therefore, the amount of material required to make the drum is $A=\frac{200}{r}+2\pi r^2$.

(b)

To determine

To find: the number of material is required

Answer to Problem 56AYU

The $A=\frac{200}{3}+18\pi$ the number of material is required

Explanation of Solution

Given:

The drum’s radius is 3 feet

Calculation:

To find the amount of the material required when drum radius is 3 feet, put $r=3$ to get

  $A=\frac{200}{r}+2\pi r^2$

  $A=\frac{200}{3}+18\pi$

Conclusion:

Therefore, the $A=\frac{200}{3}+18\pi$ number of material is required if the drum’s radius is 3 feet.

(c)

To determine

To find: the number of material is required

Answer to Problem 56AYU

The $A=50+32\pi$ number of material is required

Explanation of Solution

Given:

The drum’s radius is 4 feet

Calculation:

To find the amount of the material required when drum radius is 4 feet, put $r=4$ toget

  $A=\frac{200}{r}+2\pi r^2$

  $A=50+32\pi$

Conclusion:

Therefore, the $A=50+32\pi$ number of material is required if the drum’s radius is 4 feet.

(d)

To determine

To find: the number of material is required

Answer to Problem 56AYU

The $A=40+50\pi$ number of material is required

Explanation of Solution

Given:

The drum’s radius is 5 feet

Calculation:

To find the amount of the material required when drum radius is 4 feet, put $r=5$ toget

  $A=\frac{200}{r}+2\pi r^2$

  $A=40+50\pi$

Conclusion:

Therefore, the $A=40+50\pi$ number of material is required if the drum’s radius is 5 feet.

(e)

To determine

To graph: $A=A\left(r\right)$ and find value of r whereA should be smallest.

Answer to Problem 56AYU

The graph that the value of r at which A is minimum is $r=2.51$ .

Explanation of Solution

Calculation:

  

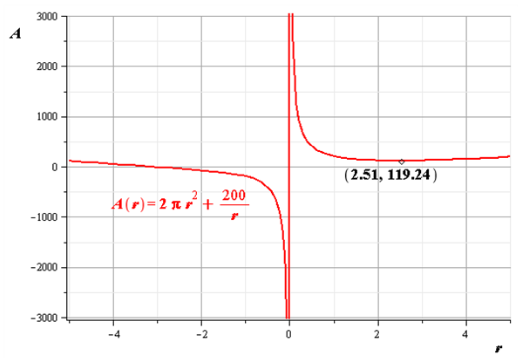
It can be clearly seen from the graph that the value of r at which A is minimum is $r=2.51$ .

Conclusion:

Therefore,the graph that the value of r at which A is minimum is $r=2.51$ .