Chapter 4.5, Problem 95AYU

Mixed Practice In Problems $93-104$, grapheach polynomial function.

$f\left(x\right)=x^4+x^2-2$

To determine

To graph: The polynomial function $f\left(x\right)=x^4+x^2-2$

Explanation of Solution

Given Information:

The polynomial function $f\left(x\right)=x^4+x^2-2$

Graph:

The steps of graphing the polynomial function as follows:

Step 1: First, find the end behavior of the graph of the function $f\left(x\right)=x^4+x^2-2$

Here, the degree of the polynomial function $f\left(x\right)$ is 4.

The graph of the function $f\left(x\right)=x^4+x^2-2$ behaves like $y=x^4$ for large values of $\left|x\right|$

Step 2: Find $x$ and $y-$ intercepts of the graph of the function.

For the $y-$ intercept, substitute $x=0$ in the function $f\left(x\right)=x^4+x^2-2$

$f\left(0\right)={\left(0\right)}^4+{\left(0\right)}^2-2=-2$

Thus, the $y-$ intercept of the polynomial function is $-2$.

For the $x-$ intercept, that is, zeros of the function, use the Rational Zeros Theorem.

$f\left(x\right)=x^4+x^2-2=0$

Since there is 1 variation in the sign of the non-zero coefficients of $f\left(x\right)$, hence, by using the Descartes’ Rule of Signs, there is 1 or 0 positive real zero.

$f\left(-x\right)={\left(-x\right)}^4+{\left(-x\right)}^2-2$

$\Rightarrow f\left(-x\right)=x^4+x^2-2$

There is 1 variation in the sign of the non-zero coefficients of $f\left(-x\right)$, hence, by using the Descartes’ Rule of Signs, there is 1 or 0 negative real zero.

By using the Rational Zero Theorem, all possible rational zeroes are of the form $x=\frac{p}{q}$, where $p$ means all factors of the constant term in the polynomial and $q$ means all factors of the leading term of the polynomial.

In the polynomial $f\left(x\right)=x^4+x^2-2$, the constant term is $-2$ and the leading term is 1.

Factors of the constant term $p=2$ are $\pm 1,\pm 2$

Factors of the leading term $q=1$ are $\pm 1$.

Therefore, all the possible rational zeros are:

$\frac{p}{q}:$ $\pm \frac{1}{1},\pm \frac{2}{1}$.

Simplifies to,

$\frac{p}{q}:\pm 1,\pm 2$.

As there is 1 or 0 positive and 1 or 0 negative real zero, all potential rational zeros of the polynomial function $f\left(x\right)=x^4+x^2-2$ are $x=\pm 1,\pm 2$ $$

Now, test $x=1$ using the synthetic division.

$\begin{array}{l}1\overline{)1010-2}\\ \underset{\_}{1122}\\ 11220\end{array}$

Here, since the remainder is 0, $x=1$ is a zero of $f$ and $\left(x-1\right)$ is a factor of $f$

To write the factors of $f$, use the entries in the bottom row of the above synthetic division.

$f\left(x\right)=x^4+x^2-2=\left(x-1\right)\left(x^3+x^2+2x+2\right)$

Here, $f\left(x\right)=x^3+x^2+2x+2$ is called a depressed equation.

Any solution to this depressed equation is also a zero of $f$, so now find zeros of this depressed equation.

The depressed equation $f\left(x\right)=x^3+x^2+2x+2=0$ can be factored as follows:

$x^3+x^2+2x+2=x^2\left(x+1\right)+2\left(x+1\right)=0$

$\Rightarrow \left(x^2+2\right)\left(x+1\right)=0$

$\Rightarrow \left(x^2+2\right)=0$ and $x+1=0$

$\Rightarrow x^2=-2$ and $x=-1$

$x^2=-2$ does not give a real solution.

Thus, the real zeros of the polynomial function $f\left(x\right)=x^4+x^2-2$ are $x=1,-1$.

Step 3: The maximum number of turning points on the graph of the function $f\left(x\right)=x^4+x^2-2$ are $4-1=3$, since the polynomial function has degree 4

The polynomial function $f\left(x\right)=x^4+x^2-2$ has degree 4 and two real zeros at $x=-1$ and $x=1$ hence, the graph crosses the $x$-axis at $x=-1$ and $x=1$.

Step 4: Now, use the information obtained in step 1 to 3 to draw the graph of the function $f\left(x\right)$ as follows:

Now, find additional points on the graph.

For $x=2$, the value of $f\left(x\right)$, at $x=2$, is $f\left(2\right)={\left(2\right)}^4+{\left(2\right)}^2-2=18$.

For $x=-2$, the value of $f\left(x\right)$, at $x=-2$, is $f\left(-2\right)={\left(-2\right)}^4+{\left(-2\right)}^2-2=18$.

Now, plot all these coordinates $\left(2,18\right)$ and $\left(-2,18\right)$ on the graph and join them.

So, the graph of the function is as follows:

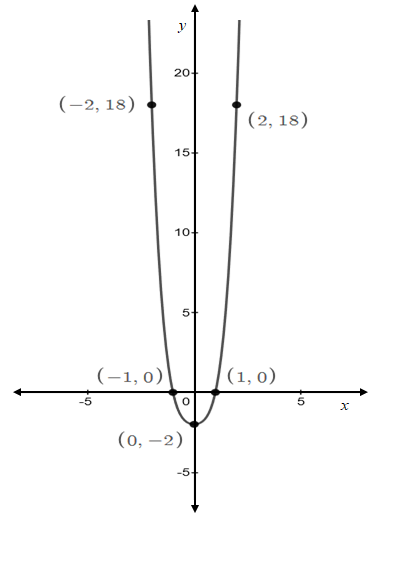
Interpretation:

The graph represents the polynomial function $f\left(x\right)=x^4+x^2-2$