Chapter 4.3, Problem 53AYU

(a)

To determine

To express:the surface area $S$ of the box as a function of $x$ .

Answer to Problem 53AYU

The required function is $S=2x^2+\frac{40000}{x}$

Explanation of Solution

Given:

Volume = 10,000 cubic inches.

  

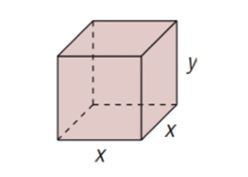
Calculation:

From the information, find the function of surface area:

Let $x$ be its base length and $y$ be its height

  $\begin{array}{l}{x}^{2}y=10000\\ y=\frac{10000}{x^2}\mathrm{..........}\left(1\right)\end{array}$

Now

  $\begin{array}{l}S=x^2+x^2+xy+xy+xy+xy\\ =2x^2+4xy\mathrm{................}\left(2\right)\end{array}$

From $\left(1\right)and\left(2\right)$ we have

  $S=2x^2+\frac{40000}{x}$

Conclusion:

The required function is $S=2x^2+\frac{40000}{x}$

(b)

To determine

To graph:the function by using a graphing utility

Answer to Problem 53AYU

  

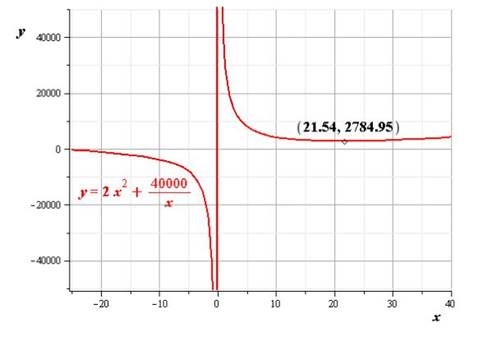
Explanation of Solution

Calculation:

  

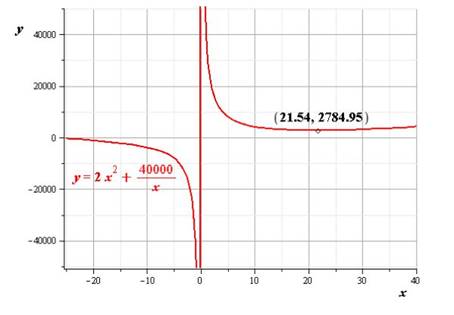
Conclusion:

Thus, the graph is drawn.

(c)

To determine

To find:the minimum amount of cardboard

Answer to Problem 53AYU

The minimum amount of cardboard is $SA=1392.446$

Explanation of Solution

Calculation:

Minima of the graph is at the point

  $\left(x,y\right)=\left(21.5444,2784.95\right)$

Now the surface area is

  $\begin{array}{l}SA=2{\left(21.544\right)}^2+\frac{10000}{21.544}\\ SA=1392.446\end{array}$

Conclusion:

The minimum amount of cardboard is $SA=1392.446$

(d)

To determine

To find:the dimensions of the box that minimize the surface area

Answer to Problem 53AYU

The dimensions of the box is $\left(x,y\right)=\left(21.544,2784.95\right)$

Explanation of Solution

Calculation:

  

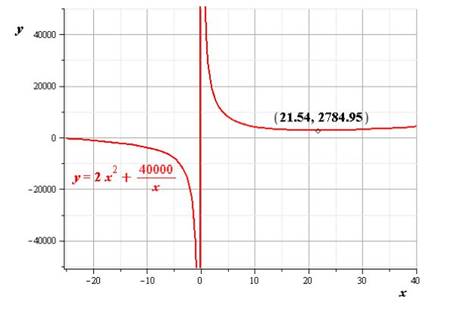
Minima of the graph is at the point

  $\left(x,y\right)=\left(21.5444,2784.95\right)$

Therefore, the dimensions of the box that minimizes the surface area

  $\left(x,y\right)=\left(21.544,2784.95\right)$

Conclusion:

The dimensions of the box is $\left(x,y\right)=\left(21.544,2784.95\right)$

(e)

To determine

To explain: the reason for showing the interest to design a box by UPS

Answer to Problem 53AYU

Minimizing the surface area will save the cost of cardboard used per square centimeter

Explanation of Solution

Calculation:

Minimizing the surface area will save the cost of cardboard used per square centimeter.