Chapter 4, Problem 91RE

(a)

To determine

To find: whether the degree of the polynomial even or odd or not

Answer to Problem 91RE

Hence the degree of this polynomial is even.

Explanation of Solution

Given:

  

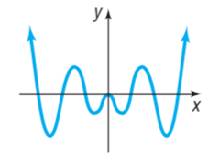
Calculation:

Recall that an even-degree polynomial are either pointing "up" on both ends or "down" on both ends. Hence the degree of this polynomial is even.

Conclusion:

Hence the degree of this polynomial is even.

(b)

To determine

To find:whether the leading coefficient positive or negative or not

Answer to Problem 91RE

Therefore the coefficient is positive .

Explanation of Solution

Calculation:

From the graph, show the beginning and the end of the graph are pointing upward,

Hence it is opening upwards, and therefore the coefficient is positive.

Conclusion:

Therefore the coefficient is positive

(c)

To determine

To find:whether the function even, odd, or neither or not

Answer to Problem 91RE

Hence, the function is even.

Explanation of Solution

Calculation:

Recall that an even function is defined when $f(x)=f(-x)$ . Since this function issymmetric about $y$ -axis. Hence the value on the left side of $y$ -axis equals the value onthe right side of $y$ -axis for a given $x$ .

Hence, the function is even.

Conclusion:

Hence, the function is even.

(d)

To determine

To find:Why $x^2$ is necessarily a factor of the polynomial

Answer to Problem 91RE

Thus, $x^2$ must be a factor.

Explanation of Solution

Calculation: Looking at the function, the graph touches the $x$ -axis 7 times, however our conclusion in parta) conclude that this is an even-degree polynomial. Since the graph touches $(0,0),$ which means 0 is a zero for this function with at least 2 multiplicity. Thus, $x^2$ must be a factor.

Conclusion:

Thus, $x^2$ must be a factor.

(e)

To determine

To find: the minimum degree of the polynomial

Answer to Problem 91RE

Hence the minimum degree of the polynomial is 8.

Explanation of Solution

Calculation:

Looking at the function, the graph touches the $x$ -axis 7 times, however our conclusion in parta) conclude that this is an even-degree polynomial. Hence the minimum degree of thepolynomial is 8.

Conclusion:

Hence the minimum degree of the polynomial is 8.

(f)

To determine

To find:the similarities and the differences

Answer to Problem 91RE

The roots for one pair of term are opposite, as well as three positive and three negative roots.

Explanation of Solution

Calculation:

To come up with the polynomial, make sure each polynomial contains at aterm $x^2$ and the roots for one pair of term are opposite, as well as three positive and threenegative roots.

  $y_1=x^2(x-1)(x-2)(x-3)(x+1)(x+2)(x+3)$

  $y_2=x^2(x-2)(x-3)(x-4)(x+2)(x+3)(x+4)$

  $y_3=x^2(x-3)(x-4)(x-5)(x+3)(x+4)(x+5)$

  $y_4=x^2(x-2)(x-4)(x-6)(x+2)(x+4)(x+6)$

  $y_5=x^2(x-1)(x-3)(x-5)(x+1)(x+3)(x+5)$

Conclusion:

Therefore, the roots for one pair of term are opposite, as well as three positive and three negative roots.