Power System Analysis and Design (MindTap Course List)
6th Edition
ISBN: 9781305632134
Author: J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3, Problem 3.25P
Consider a single-phase electric system shown in Figure 3.33. Transformers are rated as follows:
With the base in circuit Y chosen as
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A linear electrical load draws 11 A at a 0.72 lagging power factor./1 153. When a capacitor is connected, the line current dropped to 122 A and the power factor
improved to 0.98 lagging. Supply frequency is 50 Hz.
a. Let the current drawn from the source before and after introduction of the capacitor be 11 and 12
respectively. Take the source voltage as the reference and express 11 and 12 as vector
quantities in polar form.
b. Obtain the capacitor current, IC = 12 - 11, graphically as well as using complex number
manipulation. Compare the results.
c. Express the waveforms of the source current before (11(t)) and after (12(t)) introduction of the
capacitor in the form Im sin(2лft + 0). Hand sketch them on the same graph. Clearly label your
plots.
d. Analytically solve i2(t) – i1(t) using the theories of trigonometry to obtain the capacitor current
in the form, ¡C(t) = ICm sin(2πft + OC). Compare the result with the result in Part b.
Transmission line data:Data:• Active power of the load (P): 50 kW• Power factor of the load (PF): 0.8 (lagging)• Line-to-line voltage at the load (V_LC): 13.8 kV• Line resistance (R): 2 Ω• Line inductance (L): 0.8 H• Line capacitance (C): 0.0003 F• Required series compensation: 60% of the line impedance.• Line length: 250 kmDetermine:1. Characteristic impedance and propagation constant.2. The generalized long line constants A, B, C, D.3. Total voltage, current and power at the generating end.4. Voltage regulation.5. Parameters A, B, C, D of the compensation circuit.6. New generalized constants of the power system afterseries compensation.7. Conclusion of the results obtained.
3.18
In a single-phase half-wave ac-dc converter, the average value of the load
current is 1.78 A. If the converter is operated from a 240 V, 50 Hz supply
and if the average value of the output voltage is 27% of the maximum
possible value, calculate the following, assume the load to be resistive.
(a) Load resistance
(b) Firing angle
(c) Average output voltage
(d) The rms load voltage
(e) The rms load current
(f) DC power
(g) AC power
(h) Rectifier efficiency
(i) Form factor
(j) Ripple factor
Chapter 3 Solutions
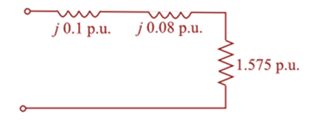
Power System Analysis and Design (MindTap Course List)
Ch. 3 - The Ohms law for the magnetic circuit states that...Ch. 3 - For an ideal transformer, the efficiency is (a) 0...Ch. 3 - For an ideal 2-winding transformer, the...Ch. 3 - An ideal transformer has no real or reactive power...Ch. 3 - For an ideal 2-winding transformer, an impedance...Ch. 3 - Consider Figure 3.4. For an ideal phase-shifting...Ch. 3 - Consider Figure 3.5. Match the following, those on...Ch. 3 - The units of admittance, conductance, and...Ch. 3 - Match the following: (i) Hysteresis loss (a) Can...Ch. 3 - For large power transformers rated more than 500...
Ch. 3 - For a short-circuit test on a 2-winding...Ch. 3 - The per-unit quantity is always dimensionless. (a)...Ch. 3 - Consider the adopted per-unit system for the...Ch. 3 - The ideal transformer windings are eliminated from...Ch. 3 - To convert a per-unit impedance from old to new...Ch. 3 - In developing per-unit circuits of systems such as...Ch. 3 - Prob. 3.17MCQCh. 3 - Prob. 3.18MCQCh. 3 - With the American Standard notation, in either a...Ch. 3 - Prob. 3.20MCQCh. 3 - In order to avoid difficulties with third-harmonic...Ch. 3 - Does an open connection permit balanced...Ch. 3 - Does an open- operation, the kVA rating compared...Ch. 3 - It is stated that (i) balanced three-phase...Ch. 3 - In developing per-unit equivalent circuits for...Ch. 3 - In per-unit equivalent circuits of practical...Ch. 3 - Prob. 3.27MCQCh. 3 - Prob. 3.28MCQCh. 3 - For developing per-unit equivalent circuits of...Ch. 3 - Prob. 3.30MCQCh. 3 - Prob. 3.31MCQCh. 3 - Prob. 3.32MCQCh. 3 - The direct electrical connection of the windings...Ch. 3 - Consider Figure 3.25 of the text for a transformer...Ch. 3 - (a) An ideal single-phase two-winding transformer...Ch. 3 - An ideal transformer with N1=1000andN2=250 is...Ch. 3 - Consider an ideal transformer with...Ch. 3 - A single-phase 100-kVA,2400/240-volt,60-Hz...Ch. 3 - Prob. 3.5PCh. 3 - Prob. 3.6PCh. 3 - Consider a source of voltage v(t)=102sin(2t)V,...Ch. 3 - Prob. 3.8PCh. 3 - Prob. 3.9PCh. 3 - A single-phase step-down transformer is rated...Ch. 3 - For the transformer in Problem 3.10. The...Ch. 3 - Prob. 3.12PCh. 3 - A single-phase 50-kVA,2400/240-volt,60-Hz...Ch. 3 - A single-phase 50-kVA,2400/240-volt,60-Hz...Ch. 3 - Rework Problem 3.14 if the transformer is...Ch. 3 - A single-phase, 50-kVA,2400/240-V,60-Hz...Ch. 3 - The transformer of Problem 3.16 is supplying a...Ch. 3 - Using the transformer ratings as base quantities,...Ch. 3 - Using the transformer ratings as base quantities....Ch. 3 - Using base values of 20 kVA and 115 volts in zone...Ch. 3 - Prob. 3.21PCh. 3 - A balanced Y-connected voltage source with...Ch. 3 - Figure 3.32 shows the oneline diagram of a...Ch. 3 - For Problem 3.18, the motor operates at full load,...Ch. 3 - Consider a single-phase electric system shown in...Ch. 3 - A bank of three single-phase transformers, each...Ch. 3 - A three-phase transformer is rated...Ch. 3 - For the system shown in Figure 3.34. draw an...Ch. 3 - Consider three ideal single-phase transformers...Ch. 3 - Reconsider Problem 3.29. If Va,VbandVc are a...Ch. 3 - Prob. 3.31PCh. 3 - Determine the positive- and negative-sequence...Ch. 3 - Consider the three single-phase two-winding...Ch. 3 - Three single-phase, two-winding transformers, each...Ch. 3 - Consider a bank of this single-phase two-winding...Ch. 3 - Three single-phase two-winding transformers, each...Ch. 3 - Three single-phase two-winding transformers, each...Ch. 3 - Consider a three-phase generator rated...Ch. 3 - The leakage reactance of a three-phase,...Ch. 3 - Prob. 3.40PCh. 3 - Consider the single-line diagram of the power...Ch. 3 - For the power system in Problem 3.41, the...Ch. 3 - Three single-phase transformers, each rated...Ch. 3 - A 130-MVA,13.2-kV three-phase generator, which has...Ch. 3 - Figure 3.39 shows a oneline diagram of a system in...Ch. 3 - The motors M1andM2 of Problem 3.45 have inputs of...Ch. 3 - Consider the oneline diagram shown in Figure 3.40....Ch. 3 - With the same transformer banks as in Problem...Ch. 3 - Consider the single-Line diagram of a power system...Ch. 3 - A single-phase three-winding transformer has the...Ch. 3 - The ratings of a three-phase three-winding...Ch. 3 - Prob. 3.52PCh. 3 - The ratings of a three-phase, three-winding...Ch. 3 - An infinite bus, which is a constant voltage...Ch. 3 - A single-phase l0-kVA,2300/230-volt,60-Hz...Ch. 3 - Three single-phase two-winding transformers, each...Ch. 3 - A two-winding single-phase transformer rated...Ch. 3 - A single-phase two-winding transformer rated...Ch. 3 - Prob. 3.59PCh. 3 - PowerWorid Simulator case Problem 3_60 duplicates...Ch. 3 - Rework Example 3.12 for a+10 tap, providing a 10...Ch. 3 - A 23/230-kV step-up transformer feeds a...Ch. 3 - The per-unit equivalent circuit of two...Ch. 3 - Reconsider Problem 3.64 with the change that now...Ch. 3 - What are the advantages of correctly specifying a...Ch. 3 - Why is it important to reduce the moisture within...Ch. 3 - What should be the focus of transformer preventive...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Disassemmble In another way f(t) = [sin(200πt) - cos(300πt)]2arrow_forward☑ 口 ☐ : Homework help starts here! Home | bartleby → https://www.bartleby.com Answered: Decompose using relationships 3 S(+) = 50 sin 3 (500πiz) | bartleby ASK AN EXPERT √ MATH SOLVER Decompose using relationships 3 S(+) = 50 sin 3 (500... Steps "Disassemble in another way." f(+)= 50 Sin³ (500+) Step 1 To decompose f(t)=50 Sin³ (500x+), use trigonometric indentity for Sin³ (e) Sin³ (0)- 3 Sin (e)-Sin (30) 4 Step2: Apply indentity to f(t). f(+)= 50 Sin³ (500+) = 50. 3 Sin (500+) - Sin (3*500π+) = 50. = = 12.5 4 3 Sin (500+)-Sin (1500+) 4 [3 Sin (580x+)-Sin (1500x+)] 37.5 Sin (500+)-12.5 Sin (1500π+) final decomposed form is, PM 05:2 19/12/2024 દ ))^ C W E × م اكتب هنا للبحثarrow_forward6) The principal of DIT hire you to design PBAX with 120 phones. Assuming the number of call is 3/hour/line, the average call duration is 4 minutes, and 55% of all call are made external via a T-1 trunk (24 channels) to the PSTN. Determine carried traffic and channel usage.arrow_forward
- Need a solufor number 2arrow_forwardDecompose using relationships 3 S(+) = 50 sin ³ (500πiz)arrow_forwardA linear electrical load draws I₁ A at a 0.72 lagging power factor. 11 = 153 When a capacitor is connected, the line current dropped to 122 A and the power factor improved to 0.98 lagging. Supply frequency is 50 Hz. a. Let the current drawn from the source before and after introduction of the capacitor be 1₁ and 12 respectively. Take the source voltage as the reference and express 11 and 12 as vector quantities in polar form. b. Obtain the capacitor current, Ic = I2 − I₁, graphically as well as using complex number manipulation. Compare the results. c. Express the waveforms of the source current before (i₁(t)) and after (i2(t)) introduction of the capacitor in the form Im sin(2лft + 0). Hand sketch them on the same graph. Clearly label your plots. d. Analytically solve i₂ (t) - i₁ (t) using the theories of trigonometry to obtain the capacitor current in the form, ic (t) = 1cm sin(2´ft + 0c). Compare the result with the result in Part b.arrow_forward
- I need a solution from an expert without artificial intelligence. Choose the correct answer 1. The convolution of two signals in time domain is equivalent to (addition, subtraction, multiplication, division). 2. The Fourier transform of non-periodic signal is random). 3. In ASK). in frequency domain signal. (discrete, continuous, digital, the pulse location is proportional to the amplitude of the signal. (PAM, PWM, PPM 4. In TDM the input signals must have (the same maximum frequency, the same sampling frequency, the same bit rate, the same amplitude). 5. The Delta Modulation is equivalent to (1-bit DPCM, 2-bit DPCM, n-bit PCM, PSK). bandwidth when compared to the NRZ 6. In baseband digital transmission, the RZ signal has signal. (less, greater, equal, not related). 7. In Differential Manchester code, the shapes of "1" and "0" are, each other, next bit dependent, not related to each other). (the same, opposite to 8. In multi-level digital carrier system R, is _ R₁. (equal to, less…arrow_forwardI need a solution from an expert without artificial intelligence. Choose the correct answer: 1. In AMI code, the shapes of "1" and "O" are, bit dependent, not related to each other). 2. In FDM the guard band is used to decrease, maintain, not related to). 3. Higher number of levels in PCM produces (the same, opposite to each other, next the overlap between FDM signals. (increase, (higher quantization error, less number of bits per sample, lower quantization error, the same number of bits per sample). 4. If the maximum shift in frequency is 70 kHz and the minimum deviation in frequency of the actual signal is 109.93 MHz, what is the carrier frequency? (110 MHz, 110 kHz, 107 kHz, 102 MHz) Fc 5. TDM of signals requires them to have the same amplitude, sampling frequency, energy). 6. In standard AM, the last step in the transmitter is subtracting, multiplying, dividing). . In digital carrier systems, PSK). (maximum frequency, maximum the carrier signal. (adding, has higher bandwidth. (ASK,…arrow_forwardNeed Handwritten solution step by steparrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Power System Analysis and Design (MindTap Course ...Electrical EngineeringISBN:9781305632134Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. SarmaPublisher:Cengage Learning
Power System Analysis and Design (MindTap Course ...
Electrical Engineering
ISBN:9781305632134
Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma
Publisher:Cengage Learning
Y Parameters - Admittance Parameters; Author: Electrical Engineering Authority;https://www.youtube.com/watch?v=MLqqa8YbVrA;License: Standard Youtube License