Chapter 2.6, Problem 17AYU

To determine

To find: To express the Area $A$ within the circle, but outside the triangle, as a function of the length $x$ of side of an equilateral triangle, inscribed inside the circle.

Answer to Problem 17AYU

Solution:

$A\left(x\right)=\left(\frac{\pi }{3}-\frac{\sqrt{3}}{4}\right)x^2$

Explanation of Solution

Given:

An equilateral triangle of side ‘$x$’ is inscribed inside a circle of radius ‘$r$’ as given below.

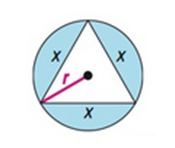
Calculation:

To express the Area $A$ within the circle, but outside the triangle, as a function of the length $x$ of side of an equilateral triangle, inscribed inside the circle.

Area of a circle of radius $r,A_1=\pi r^2$.

Area of an equilateral triangle of side $x,A_2=\frac{\sqrt{3}}{4}{x}^2$.

Area that is within the circle but outside the triangle $A=A_1-A_2$.

To represent radius $r$ interms of $x$.

When an equilateral triangle is inscribed inside a circle, then the centre of the circle matches with the centroid of the triangle.

If $x=$ side of the triangle then, height of the equilateral triangle $=\frac{\sqrt{3}}{2}x$.

Now, centroid of a triangle divides the height in the ratio 2:1.

Therefore, the distance between centroid to any vertices of the equilateral triangle $=2/3$ of height of the equilateral triangle.

$r=\frac{2}{3}\times \left(\frac{\sqrt{3}}{2}x\right)$

$r=\frac{1}{\sqrt{3}}x$

The area $A_1$ of the circle is $A_1\left(x\right)=\pi r^2=\pi \frac{x^2}{3}$.

Area that is within the circle but outside the triangle $A=A_1-A_2=\pi \frac{x^2}{3}-\frac{\sqrt{3}}{4}{x}^2$.

Therefore, $A\left(x\right)=\left(\frac{\pi }{3}-\frac{\sqrt{3}}{4}\right)x^2$.