Chapter 2, Problem 40RE

To determine

To answer:

a. The questions related to the volume of a square box whose volume is 10 cubic feet.

Answer to Problem 40RE

Solution:

a. $A\left(x\right)=2x^2+\frac{40}{x}$

Explanation of Solution

Given:

$V=10$ cubic meter.

Calculation:

a. Amount $A$ of material used to make a box with square base:

Let $x$ and $y$ be the length and height of the box.

It is given that the volume of the box with square base is 10 cubic feet. So,

$10=x^2\times y$

Thus, the height of the box is

$y=\frac{10}{x^2}$

Now, the amount of material required to build the box is equal to the surface area of the box.

Surface area of the box is

$A=2x^2+4xy$

Substituting $y=\frac{10}{x^2}$, we get

$A=2x^2+4x\cdot \frac{10}{x^2}$

$A=2x^2+\frac{40}{x}$

Thus, $A\left(x\right)=2x^2+\frac{40}{x}$.

To determine

To answer:

b. The questions related to the volume of a square box whose volume is 10 cubic feet.

Answer to Problem 40RE

Solution:

b. $A=42$ square feet.

Explanation of Solution

Given:

$V=10$ cubic meter.

Calculation:

b. Material required for a base of 1 foot by 1 foot:

Substituting $x=1$, we get

$A\left(1\right)=2{\left(1\right)}^2+\frac{40}{\left(1\right)}$

$A\left(1\right)=42$ square feet.

To determine

To answer:

c. The questions related to the volume of a square box whose volume is 10 cubic feet.

Answer to Problem 40RE

Solution:

c. $A=28$ square feet.

Explanation of Solution

Given:

$V=10$ cubic meter.

Calculation:

c. Material required for a base of 2 foot by 2 foot:

Substituting $x=2$, we get

$A\left(2\right)=2{\left(2\right)}^2+\frac{40}{\left(2\right)}$

$A\left(2\right)=28$ square feet.

To determine

To answer:

d. The questions related to the volume of a square box whose volume is 10 cubic feet.

Answer to Problem 40RE

Solution:

d. $x=2.154$ feet.

Explanation of Solution

Given:

$V=10$ cubic meter.

Calculation:

d. Graph:

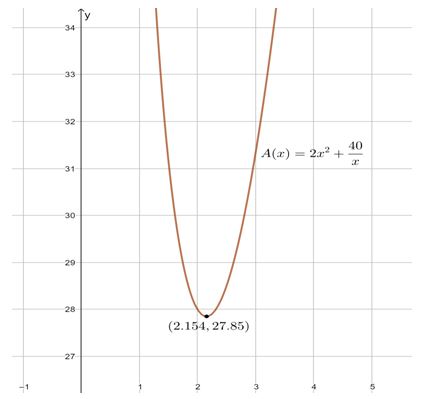
From the graph, we find that the smallest area is $27.85$ square feet for the value of $x=2.154$ feet.