Chapter 2.3, Problem 28AYU

In Problems 25-32, the graph of a function is given. Use the graph to find:

a. The intercepts, if any

b. The domain and range

c. The intervals on which the function is increasing, decreasing, or constant

d. Whether the function is even, odd, or neither

32.

To determine

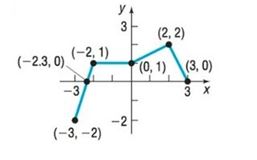
To find: The following values using the given graph:

a. Intercepts($x$ and $y$ intercepts)

b. The domain and range set of the function.

c. Increasing intervals, decreasing intervals and constant interval if any.

d. Nature of the function (even, odd or neither).

Answer to Problem 28AYU

From the graph, concluding the following results:

a. Intercepts($x$ and $y$ intercepts)

$\text{The }x\text{-intercepts are }-2.3\text{ and <mn>3</mn>; the }y\text{-intercepts is 1}$.

b. The domain and range set of the function.

The domain of $f$ is $\left\{x/-3\le x\le \text{ 3}\right\}$ or the interval $\left[-3,\text{ 3}\right]$.

The range of $f$ is $\left\{x/-2\le x\le \text{ 2}\right\}$ or the interval $\left[-2,\text{ 2}\right]$.

c. The function $f$ is increasing in the interval $\left[-3,-2\right]\text{ and }\left[0,2\right]$, decreasing in the interval $\left[2,\text{ 3}\right]$ and it is constant in the interval $\left[-2,\text{ 0}\right]$ in the given graph.

d.The given function is neither even nor odd.

Explanation of Solution

Given:

It is asked to find the intercepts ($x$ and $y$ if any), domain and range, increasing intervals, decreasing intervals, and constant intervals of the function using the graph. Also, check whether the function is even, odd or neither.

Graph:

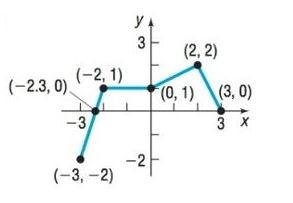
Interpretation:

a. Intercepts($x$ and $y$ intercepts): The points, if any, at which a graph crosses or touches the coordinate axes are called the intercepts.

The $x\text{-coordinate}$ of a point at which the graph crosses or touches the $x\text{-axis}$ is an $x\text{-intercept}$, and the $y\text{-coordinate}$ of a point at which the graph crosses or touches the $y\text{-axis}$ is an $y\text{-intercept}$.

The intercepts of the graph are the points

$\left(-2.3,0\right),\left(0,1\right)$and $\left(3,\text{ 0}\right)$

The $x\text{-intercepts}$ are $-2.3$ and $3$; the $y\text{-intercepts}$ is $1$

b. The domain and range set of the function.

To determine the domain of $f$ notice that the points on the graph of $f$ have $x\text{-coordinates}$ between $-3$ and $\text{3}$, inclusive; and for each number $x$ between $-3$ and $\text{3}$, there is a point $\left(x,f\left(x\right)\right)$ on the graph. The domain of $f$ is $\left\{x/-3\le x\le \text{ 3}\right\}$ or the interval $\left[-3,\text{ 3}\right]$

The points on the graph all have $y\text{-coordinates}$ between $-2$ to $\text{2}$ inclusive; and for each such number $y$ there is at least one number $x$ in the domain. The range of $f$ is $\left\{x/-2\le x\le \text{ 2}\right\}$ or the interval $\left[-2,\text{ 2}\right]$.

c. Increasing intervals, decreasing intervals and constant interval if any.

It can be directly concluded from the graph that the curve is increasing from $-3$ to $-2$, then it is constant from $-2$ to $\text{0}$, then it is increasing from $\text{0}$ to $\text{2}$ , then at last it is decreasing from $\text{2}$ to $\text{3}$.

Therefore, the function $f$ is increasing in the interval $\left[-3,-2\right]$ and $\left[0,\text{ 2}\right]$, decreasing in the interval$\left[2,\text{ 3}\right]$ and it is constant in the interval $\left[-2,\text{ 0}\right]$ in the given graph.

d. Nature of the function (even, odd or neither).

By the theorem of test for symmetry, “A function is even if and only if its graph is symmetric with respect to the $y\text{-axis}$. A function is odd if and only if its graph is symmetric with respect to the origin”.

It can be easily concluded from the graph that it is neither symmetric with respect to $x\text{-axis}$ nor symmetric with respect to $y\text{-axis}$.

Therefore, the given function is neither even nor odd.