Chapter 2.5, Problem 37E

a.

To determine

To find: Formula for the sum of two measurements

Answer to Problem 37E

The sum of two population measurements is $P\left(t\right)=2-2t+2t^2$ .

Explanation of Solution

Given:

A population of bacteria consists of two types a , b which grow with time according to relation $a\left(t\right)=1+t^2$ , $b\left(t\right)=1-2t+t^2$ where population is measured in millions and the time t in hours. The total population is $P\left(t\right)=a\left(t\right)+b\left(t\right)$ .

Formula used:

The formula for sum of two quantities.

Calculation:

The two measurements of bacteria populations are $a\left(t\right)=1+t^2$ and $b\left(t\right)=1-2t+t^2$ .

The sum of two population measurements is $\text{S}=a\left(t\right)+b\left(t\right)=1+t^2+1-2t+t^2=2-2t+2t^2$ .

Conclusion:

The sum of two population measurements is $P\left(t\right)=2-2t+2t^2$ .

b.

To determine

To find:The derivative of each component of bacteria population.

Answer to Problem 37E

The derivatives of population measurements components are $a^{\prime }\left(t\right)=2t$ and $b^{\prime }\left(t\right)=-2+2t$ .

Explanation of Solution

Given:

The two population measurement components $a\left(t\right)$ and $b\left(t\right)$ in part (a)

Formula used:

The derivative of function $y\left(t\right)=t^n$ is $\frac{dy}{dt}=n{t}^{n-1}$

Calculation:

The population components are $a\left(t\right)=1+t^2$ , and $b\left(t\right)=1-2t+t^2$

Their derivatives are

$\frac{da}{dt}=a^{\prime }\left(t\right)=\frac{d\left(1\right)}{dt}+\frac{d\left(t^2\right)}{dt}=0+2t=2t$ , $\frac{db}{dt}=b^{\prime }\left(t\right)=\frac{d\left(1\right)}{dt}+\frac{d\left(-2t\right)}{dt}+\frac{d\left(t^2\right)}{dt}=0-2+2t=-2+2t$

Conclusion:

The derivatives of population measurements components are $a^{\prime }\left(t\right)=2t$ and $b^{\prime }\left(t\right)=-2+2t$ .

c.

To determine

To find: The derivative of the sum and check that the sum rule works.

Answer to Problem 37E

The derivative of the sum is $P^{\prime }\left(t\right)=-2+4t=a^{\prime }\left(t\right)+b^{\prime }\left(t\right)$ that shows the sum rule works.

Explanation of Solution

Given:

The sum of population components is $P\left(t\right)=2-2t+2t^2$ .

Concept used:

The sum rule of derivatives is $\frac{d\left(u+v\right)}{dx}=\frac{d\left(u\right)}{dx}+\frac{d\left(u\right)}{dx}$ .

Calculation:

The sum of population components is $P\left(t\right)=2-2t+2t^2$ . Its derivative is

  $\frac{dP}{dt}=P^{\prime }\left(t\right)=\frac{d\left(2\right)}{dt}+\frac{d\left(-2t\right)}{dt}+\frac{d\left(2t^2\right)}{dt}$

  $\Rightarrow P^{\prime }\left(t\right)=0+-2+4t=-2+4t$

Now, the sum of derivatives of measurement components is

  $a^{\prime }\left(t\right)+b^{\prime }\left(t\right)=\left(2t\right)+\left(-2+2t\right)=-2+4t=P^{\prime }\left(t\right)$ .

Thus, we have $P^{\prime }\left(t\right)=a^{\prime }\left(t\right)+b^{\prime }\left(t\right)$ . This shows the sum rule follows.

Conclusion:

The derivative of the sum is $P^{\prime }\left(t\right)=-2+4t=a^{\prime }\left(t\right)+b^{\prime }\left(t\right)$ that shows the sum rule works.

d.

To determine

To describe: In words what is happening.

Answer to Problem 37E

The population of bacteria represented by the component $a\left(t\right)$ increases.

The population of bacteria represented by the component $b\left(t\right)$ decreases for first hour and then increases.

The overall population of bacteria represented by the component $b\left(t\right)$ decreases for first half an hour and then increases.

Explanation of Solution

Given:

The components of population measurements are $a\left(t\right)=1+t^{2}b$ and $b\left(t\right)=1-2t+t^2$ , and their sum is $P\left(t\right)=2-2t+2t^2$ .

Concept used:

The function $y=f\left(t\right)$ is increasing in an interval $\left[a,b\right]$ if $f^{\prime }\left(t\right)>0$

$\forall t\in \left[a,b\right]$ and decreasing if $f^{\prime }\left(t\right)<0$

  $\forall t\in \left[a,b\right]$ .

Calculation:

Since $a^{\prime }\left(t\right)=2t$ always positive (as t is the time), i.e., $a^{\prime }\left(t\right)>0$ , hence the population of bacteria represented by the component $a\left(t\right)$ increases.

Since $b^{\prime }\left(t\right)=-2+2t$ is negative when $t<1$ , and positive when $t>1$ , hence the population of bacteria represented by the component $b\left(t\right)$ decreases for first hour and then increases.

Since $P^{\prime }\left(t\right)=-2+4t$ is negative when $t<\frac{1}{2}$ , and positive when $t>\frac{1}{2}$ , hence the overall population of bacteria represented by the component $b\left(t\right)$ decreases for first half an hour and then increases.

Conclusion:

The population of bacteria represented by the component $a\left(t\right)$ increases.

The population of bacteria represented by the component $b\left(t\right)$ decreases for first hour and then increases.

The overall population of bacteria represented by the component $b\left(t\right)$ decreases for first half an hour and then increases.

e.

To determine

To graph: The each component and total as function of time.

Explanation of Solution

Given:

The components of population measurements are $a\left(t\right)=1+t^2$ and $b\left(t\right)=1-2t+t^2$ , and their sum is $P\left(t\right)=2-2t+2t^2$ .

Method used:

The graph is sketched using graphing calculator

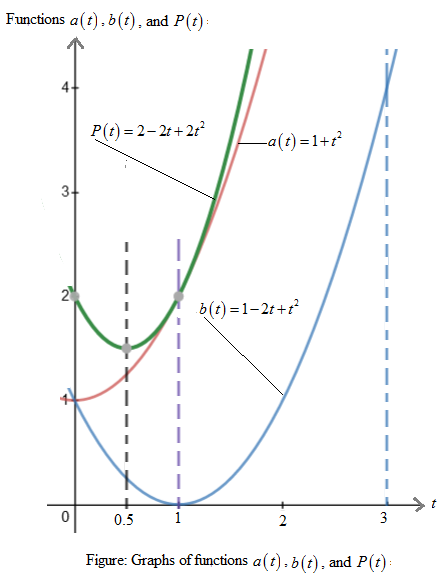
Graph:

The graphs of components of population measurements $a\left(t\right)=1+t^{2}b$ and $b\left(t\right)=1-2t+t^2$ , and of total population $P\left(t\right)=2-2t+2t^2$ in the interval $\left[0,3\right]$ are shown in figure here.