Modeling the Dynamics of Life: Calculus and Probability for Life Scientists
3rd Edition
ISBN: 9780840064189
Author: Frederick R. Adler
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2.3, Problem 28E
(a)
To determine
To sketch:The graph of the continuous function.
(a)
Expert Solution
Explanation of Solution
Given information:
A continuous function that is
Graph:
The sigma function is defined as the function which has the value -1for the negative argument, 0 when the argument is 0 and 1 for the positive argument.
The graph for the given continuous function
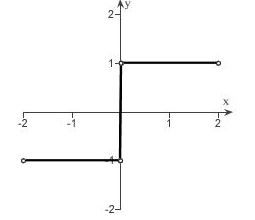
Interpretation:
From the graph it is obtained that the value -1 has negative argument and 1 has positive argument. The graph is increasing and decreasing with respect to the argument value
(b)
To determine
To find:The formula for the function.
(b)
Expert Solution
Answer to Problem 28E
The formula for the function is given below as,
Explanation of Solution
Given information:
A continuous function that is
Calculation:
To determine the formula for the function as follows,
Consider the slope for (0.01.l) as 100, and the linear function for
The formula for the function is given below as,
(c)
To determine
The inputs have to be to 0 for the output to be within 0.1 for 0.
(c)
Expert Solution
Answer to Problem 28E
The input should be within -0.001 to 0.001 for the output to be within 0.1 to 0.
Explanation of Solution
Given information:
A continuous function that is
Calculation:
The given function is
To determine the input at
Similarly, consider
From the two values of
Hence, the input should be within -0.001 to 0.001 for the output to be within 0.1 to 0.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
5. (a) State the Residue Theorem. Your answer should include all the conditions required
for the theorem to hold.
(4 marks)
(b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the
anti-clockwise direction. Evaluate
に
dz.
You must check all of the conditions of any results that you use.
(5 marks)
(c) Evaluate
L
You must check all of the conditions of any results that you use.
ཙ
x sin(Tx)
x²+2x+5
da.
(11 marks)
3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula
for L(y).
(1 mark)
(b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a
contour. Suppose there exists a finite real number M such that |f(z)| < M for
all z in the image of y. Prove that
<
||, f(z)dz| ≤ ML(y).
(3 marks)
(c) State and prove Liouville's theorem. You may use Cauchy's integral formula without
proof.
(d) Let R0. Let w € C. Let
(10 marks)
U = { z Є C : | z − w| < R} .
Let f UC be a holomorphic function such that
0 < |ƒ(w)| < |f(z)|
for all z Є U. Show, using the local maximum modulus principle, that f is constant.
(6 marks)
3. (a) Let A be an algebra. Define the notion of an A-module M. When is a module M
a simple module?
(b) State and prove Schur's Lemma for simple modules.
(c) Let AM(K) and M = K" the natural A-module.
(i) Show that M is a simple K-module.
(ii) Prove that if ƒ € Endд(M) then ƒ can be written as f(m) = am, where a
is a matrix in the centre of M, (K).
[Recall that the centre, Z(M,(K)) == {a Mn(K) | ab
M,,(K)}.]
= ba for all bЄ
(iii) Explain briefly why this means End₁(M) K, assuming that Z(M,,(K))~
K as K-algebras.
Is this consistent with Schur's lemma?
Chapter 2 Solutions
Modeling the Dynamics of Life: Calculus and Probability for Life Scientists
Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - For the following functions, find the input...Ch. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - For each of the following quadratic functions,...Ch. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - An object tossed upward at 10m/s from a height of...Ch. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.7 - Prob. 1ECh. 2.7 - Prob. 2ECh. 2.7 - Prob. 3ECh. 2.7 - Prob. 4ECh. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.8 - Prob. 1ECh. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 8ECh. 2.8 - Prob. 9ECh. 2.8 - Prob. 10ECh. 2.8 - Prob. 11ECh. 2.8 - Prob. 12ECh. 2.8 - Prob. 13ECh. 2.8 - Prob. 14ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 17ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 19ECh. 2.8 - Prob. 20ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - Prob. 23ECh. 2.8 - Prob. 24ECh. 2.8 - Prob. 25ECh. 2.8 - Prob. 26ECh. 2.8 - Prob. 27ECh. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Prob. 30ECh. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2.8 - Prob. 39ECh. 2.8 - Prob. 40ECh. 2.8 - Prob. 41ECh. 2.8 - Prob. 42ECh. 2.8 - Prob. 43ECh. 2.8 - Prob. 44ECh. 2.8 - Prob. 45ECh. 2.8 - Prob. 46ECh. 2.9 - Prob. 1ECh. 2.9 - Prob. 2ECh. 2.9 - Prob. 3ECh. 2.9 - Prob. 4ECh. 2.9 - Prob. 5ECh. 2.9 - Prob. 6ECh. 2.9 - Prob. 7ECh. 2.9 - Prob. 8ECh. 2.9 - Prob. 9ECh. 2.9 - Prob. 10ECh. 2.9 - Prob. 11ECh. 2.9 - Prob. 12ECh. 2.9 - Prob. 13ECh. 2.9 - Prob. 14ECh. 2.9 - Prob. 15ECh. 2.9 - Prob. 16ECh. 2.9 - Prob. 17ECh. 2.9 - Prob. 18ECh. 2.9 - Prob. 19ECh. 2.9 - Prob. 20ECh. 2.9 - Prob. 21ECh. 2.9 - Prob. 22ECh. 2.9 - Prob. 23ECh. 2.9 - Prob. 24ECh. 2.9 - Prob. 25ECh. 2.9 - Prob. 26ECh. 2.9 - Prob. 27ECh. 2.9 - Prob. 28ECh. 2.9 - Prob. 29ECh. 2.9 - Prob. 30ECh. 2.9 - Prob. 31ECh. 2.9 - Prob. 32ECh. 2.9 - Prob. 33ECh. 2.9 - Prob. 34ECh. 2.9 - Prob. 35ECh. 2.9 - Prob. 36ECh. 2.9 - Prob. 38ECh. 2.9 - Prob. 39ECh. 2.9 - Prob. 40ECh. 2.9 - Prob. 41ECh. 2.9 - Prob. 42ECh. 2.9 - Prob. 43ECh. 2.9 - Prob. 44ECh. 2.9 - The method of implicit differentiation is often...Ch. 2.9 - Prob. 46ECh. 2.9 - Prob. 47ECh. 2.9 - Prob. 48ECh. 2.9 - Prob. 49ECh. 2.9 - Prob. 50ECh. 2.9 - Prob. 51ECh. 2.9 - Prob. 52ECh. 2.9 - Prob. 53ECh. 2.10 - Prob. 1ECh. 2.10 - Prob. 2ECh. 2.10 - Prob. 3ECh. 2.10 - Prob. 4ECh. 2.10 - Prob. 5ECh. 2.10 - Prob. 6ECh. 2.10 - Prob. 7ECh. 2.10 - Prob. 8ECh. 2.10 - Prob. 9ECh. 2.10 - Prob. 10ECh. 2.10 - Prob. 11ECh. 2.10 - Prob. 12ECh. 2.10 - Prob. 13ECh. 2.10 - Prob. 14ECh. 2.10 - Prob. 15ECh. 2.10 - Prob. 16ECh. 2.10 - Prob. 17ECh. 2.10 - Prob. 18ECh. 2.10 - Prob. 19ECh. 2.10 - Prob. 20ECh. 2.10 - Prob. 21ECh. 2.10 - Prob. 22ECh. 2.10 - Prob. 23ECh. 2.10 - Prob. 24ECh. 2.10 - Prob. 25ECh. 2.10 - Prob. 26ECh. 2.10 - Prob. 27ECh. 2.10 - Prob. 28ECh. 2.10 - Prob. 29ECh. 2.10 - Prob. 30ECh. 2.10 - Prob. 31ECh. 2.10 - Prob. 32ECh. 2.10 - Prob. 33ECh. 2.10 - Prob. 34ECh. 2.10 - Prob. 35ECh. 2.10 - Prob. 36ECh. 2.10 - Prob. 37ECh. 2.10 - Prob. 38ECh. 2.10 - Prob. 39ECh. 2.10 - Prob. 40ECh. 2.10 - Prob. 41ECh. 2.10 - Prob. 42ECh. 2.10 - Prob. 43ECh. 2 - Prob. 1SPCh. 2 - Prob. 2SPCh. 2 - Prob. 3SPCh. 2 - Prob. 4SPCh. 2 - Prob. 5SPCh. 2 - Prob. 6SPCh. 2 - Prob. 7SPCh. 2 - Prob. 8SPCh. 2 - Prob. 9SPCh. 2 - Prob. 10SPCh. 2 - Prob. 11SPCh. 2 - Prob. 12SPCh. 2 - Prob. 13SPCh. 2 - Prob. 14SPCh. 2 - Prob. 15SPCh. 2 - Prob. 16SPCh. 2 - Prob. 17SPCh. 2 - Prob. 18SPCh. 2 - Prob. 19SPCh. 2 - Prob. 20SPCh. 2 - Prob. 21SPCh. 2 - Prob. 22SPCh. 2 - Prob. 23SPCh. 2 - Prob. 24SPCh. 2 - Prob. 25SPCh. 2 - Prob. 26SPCh. 2 - Prob. 27SPCh. 2 - Prob. 28SPCh. 2 - Prob. 29SPCh. 2 - Prob. 30SPCh. 2 - Prob. 31SPCh. 2 - Prob. 32SPCh. 2 - Prob. 33SPCh. 2 - Prob. 34SPCh. 2 - Prob. 35SPCh. 2 - Prob. 36SP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- (a) State, without proof, Cauchy's theorem, Cauchy's integral formula and Cauchy's integral formula for derivatives. Your answer should include all the conditions required for the results to hold. (8 marks) (b) Let U{z EC: |z| -1}. Let 12 be the triangular contour with vertices at 0, 2-2 and 2+2i, parametrized in the anticlockwise direction. Calculate dz. You must check the conditions of any results you use. (d) Let U C. Calculate Liz-1ym dz, (z - 1) 10 (5 marks) where 2 is the same as the previous part. You must check the conditions of any results you use. (4 marks)arrow_forward(a) Suppose a function f: C→C has an isolated singularity at wЄ C. State what it means for this singularity to be a pole of order k. (2 marks) (b) Let f have a pole of order k at wЄ C. Prove that the residue of f at w is given by 1 res (f, w): = Z dk (k-1)! >wdzk−1 lim - [(z — w)* f(z)] . (5 marks) (c) Using the previous part, find the singularity of the function 9(z) = COS(πZ) e² (z - 1)²' classify it and calculate its residue. (5 marks) (d) Let g(x)=sin(211). Find the residue of g at z = 1. (3 marks) (e) Classify the singularity of cot(z) h(z) = Z at the origin. (5 marks)arrow_forward1. Let z = x+iy with x, y Є R. Let f(z) = u(x, y) + iv(x, y) where u(x, y), v(x, y): R² → R. (a) Suppose that f is complex differentiable. State the Cauchy-Riemann equations satisfied by the functions u(x, y) and v(x,y). (b) State what it means for the function (2 mark) u(x, y): R² → R to be a harmonic function. (3 marks) (c) Show that the function u(x, y) = 3x²y - y³ +2 is harmonic. (d) Find a harmonic conjugate of u(x, y). (6 marks) (9 marks)arrow_forward
- Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b² = ab = ba = 0. (ii) a²=b, b² = ab = ba = 0. (iii) a²=b, b² = b, ab = ba = 0.arrow_forwardNo chatgpt pls will upvotearrow_forward= 1. Show (a) Let G = Z/nZ be a cyclic group, so G = {1, 9, 92,...,g" } with g": that the group algebra KG has a presentation KG = K(X)/(X” — 1). (b) Let A = K[X] be the algebra of polynomials in X. Let V be the A-module with vector space K2 and where the action of X is given by the matrix Compute End(V) in the cases (i) x = p, (ii) xμl. (67) · (c) If M and N are submodules of a module L, prove that there is an isomorphism M/MON (M+N)/N. (The Second Isomorphism Theorem for modules.) You may assume that MON is a submodule of M, M + N is a submodule of L and the First Isomorphism Theorem for modules.arrow_forward
- (a) Define the notion of an ideal I in an algebra A. Define the product on the quotient algebra A/I, and show that it is well-defined. (b) If I is an ideal in A and S is a subalgebra of A, show that S + I is a subalgebra of A and that SnI is an ideal in S. (c) Let A be the subset of M3 (K) given by matrices of the form a b 0 a 0 00 d Show that A is a subalgebra of M3(K). Ꮖ Compute the ideal I of A generated by the element and show that A/I K as algebras, where 0 1 0 x = 0 0 0 001arrow_forward(a) Let HI be the algebra of quaternions. Write out the multiplication table for 1, i, j, k. Define the notion of a pure quaternion, and the absolute value of a quaternion. Show that if p is a pure quaternion, then p² = -|p|². (b) Define the notion of an (associative) algebra. (c) Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b²=ab = ba 0. (ii) a² (iii) a² = b, b² = abba = 0. = b, b² = b, ab = ba = 0. (d) Let u1, 2 and 3 be in the Temperley-Lieb algebra TL4(8). ገ 12 13 Compute (u3+ Augu2)² where A EK and hence find a non-zero x € TL4 (8) such that ² = 0.arrow_forwardQ1: Solve the system x + x = t², x(0) = (9)arrow_forward
- Between the function 3 (4)=x-x-1 Solve inside the interval [1,2]. then find the approximate Solution the root within using the bisection of the error = 10² method.arrow_forwardE10) Perform four iterations of the Jacobi method for solving the following system of equations. 2 -1 -0 -0 XI 2 0 0 -1 2 X3 0 0 2 X4 With x(0) (0.5, 0.5, 0.5, 0.5). Here x = (1, 1, 1, 1)". How good x (5) as an approximation to x?arrow_forwardby (2) Gauss saidel - - method find (2) و X2 for the sestem X1 + 2x2=-4 2x1 + 2x2 = 1 Such thef (0) x2=-2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY