
Concept explainers
That the camera lens need to move farther away from or closer to the camera film or sensor if a photographer moves closer to his subject and then refocuses
Answer to Problem 21Q
Solution:
The camera lens moves farther from the film when the photographer refocuses.
By moving closer to the object, the object distance has become smaller, which the thin lens equation says increases the image distance (and the image is now behind the film). To bring the image forward (and back to the film), you need to move the lens away from the film.
Explanation of Solution
A camera using a thin converging lens, the ray diagram of the image forming is given by the figure.
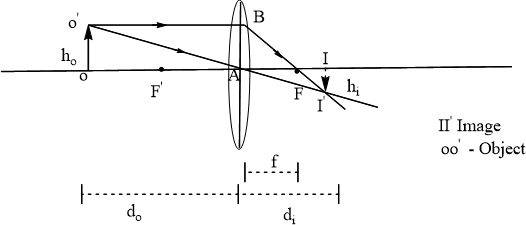
The Lens equation of the image formed by the lens is given by
Where,
The lens formula can be used to analyze the given scenario. While refocusing the camera, the camera is brought closer to the object. Hence, from the lens equation, the object distance is reduced.
If the object distance is reduced, the image distance is increased and so the image falls beyond the film position. As the film is immovable, the lens has been moved away the film and thereby increasing the image distance which will satisfy the above equation and producing the image on the film.
Chapter 23 Solutions
Physics: Principles with Applications
Additional Science Textbook Solutions
Human Biology: Concepts and Current Issues (8th Edition)
Applications and Investigations in Earth Science (9th Edition)
Anatomy & Physiology (6th Edition)
Cosmic Perspective Fundamentals
Campbell Essential Biology (7th Edition)
Campbell Biology in Focus (2nd Edition)
- A piece of metal is placed on top of a 2.0 - kg wooden block (mass density = 562 kg/m³) piece. UseArchimedes' principle to calculate the mass (in kg) of copper if the top of the wood surface is exactly at thewater's surface?arrow_forwardA filmmaker wants to achieve an interesting visual effect by filming a scene through a converging lens with a focal length of 50.0 m. The lens is placed betwen the camera and a horse, which canters toward the camera at a constant speed of 7.9 m/s. The camera starts rolling when the horse is 36.0 m from the lens. Find the average speed of the image of the horse (a) during the first 2.0 s after the camera starts rolling and (b) during the following 2.0 s.arrow_forwardAnswer the question (Physics)arrow_forward
- Hi! I need help with these calculations for part i and part k for a physics Diffraction Lab. We used a slit width 0.4 mm to measure our pattern.arrow_forwardExamine the data and % error values in Data Table 3 where the angular displacement of the simple pendulum decreased but the mass of the pendulum bob and the length of the pendulum remained constant. Describe whether or not your data shows that the period of the pendulum depends on the angular displacement of the pendulum bob, to within a reasonable percent error.arrow_forwardIn addition to the anyalysis of the graph, show mathematically that the slope of that line is 2π/√g . Using the slope of your line calculate the value of g and compare it to 9.8.arrow_forward
- An object is placed 24.1 cm to the left of a diverging lens (f = -6.51 cm). A concave mirror (f= 14.8 cm) is placed 30.2 cm to the right of the lens to form an image of the first image formed by the lens. Find the final image distance, measured relative to the mirror. (b) Is the final image real or virtual? (c) Is the final image upright or inverted with respect to the original object?arrow_forwardConcept Simulation 26.4 provides the option of exploring the ray diagram that applies to this problem. The distance between an object and its image formed by a diverging lens is 5.90 cm. The focal length of the lens is -2.60 cm. Find (a) the image distance and (b) the object distance.arrow_forwardPls help ASAParrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





