
Concept explainers
(a)
To find: The linear regression model and scatter graph.
The model of the given data
Given information
The table for the given data is below.
| period | 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 |
| temperature | 2600 | 2390 | 3310 | 3720 | 4560 | 5110 | 6860 | 8820 | 9650 |
The equation is
The values are calculated using the following table
| x | y | x2 | x3 | x4 | x·y | x2·y |
| 1 | 2600 | 1 | 1 | 1 | 2600 | 2600 |
| 6 | 2390 | 36 | 216 | 1296 | 14340 | 86040 |
| 11 | 3310 | 121 | 1331 | 14641 | 36410 | 400510 |
| 16 | 3720 | 256 | 4096 | 65536 | 59520 | 952320 |
| 21 | 4560 | 441 | 9261 | 194481 | 95760 | 2010960 |
| 26 | 5110 | 676 | 17576 | 456976 | 132860 | 3454360 |
| 31 | 6860 | 961 | 29791 | 923521 | 212660 | 6592460 |
| 36 | 8820 | 1296 | 46656 | 1679616 | 317520 | 11430720 |
| 41 | 9650 | 1681 | 68921 | 2825761 | 395650 | 16221650 |
| --- | --- | --- | --- | --- | --- | --- |
| ∑x=189 | ∑y=47020 | ∑x·y=1267320 |
Substituting these values in the normal equations
9a+189b+5469c=47020
189a+5469b+177849c=1267320
5469a+177849b+6161829c=41151620
Solving these 3 equations,
Total Equations are 3
9a+189b+5469c=47020→(1)
189a+5469b+177849c=1267320→(2)
5469a+177849b+6161829c=41151620→(3)
Select the equations (1) and (2), and eliminate the variable a.

Select the equations (1) and (3), and eliminate the variable a.

Select the equations (4) and (5), and eliminate the variable b.

Now use back substitution method
From (6)
577500c=2470000
⇒c=2470000577500=4.2771
From (4)
-1500b-63000c=-279900
⇒-1500b-63000(4.2771)=-279900
⇒-1500b-269454.5455=-279900
⇒-1500b=-279900+269454.5455=-10445.4545
⇒b=-10445.4545-1500=6.9636
From (1)
9a+189b+5469c=47020
⇒9a+189(6.9636)+5469(4.2771)=47020
⇒9a+24707.3481=47020
⇒9a=47020-24707.3481=22312.6519
⇒a=22312.65199=2479.1835
Solution using Elimination method.
a=2479.1835,b=6.9636,c=4.2771
Now substituting this values in the equation is
Scatter graph of the following data given below
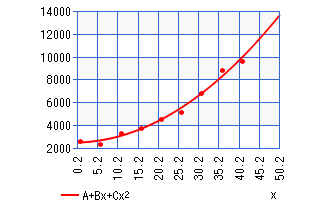
(b)
To find: The quadratic regression model and scatter graph.
The model of the given data
Given information
The table for the given data is below.
| period | 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 |
| temperature | 2600 | 2390 | 3310 | 3720 | 4560 | 5110 | 6860 | 8820 | 9650 |
The equation is
The values are calculated using the following table
| x | y | x2 | x3 | x4 | x5 | x6 | x·y | x2·y | x3·y |
| 1 | 2600 | 1 | 1 | 1 | 1 | 1 | 2600 | 2600 | 2600 |
| 6 | 2390 | 36 | 216 | 1296 | 7776 | 46656 | 14340 | 86040 | 516240 |
| 11 | 3310 | 121 | 1331 | 14641 | 161051 | 1771561 | 36410 | 400510 | 4405610 |
| 16 | 3720 | 256 | 4096 | 65536 | 1048576 | 16777216 | 59520 | 952320 | 15237120 |
| 21 | 4560 | 441 | 9261 | 194481 | 4084101 | 85766121 | 95760 | 2010960 | 42230160 |
| 26 | 5110 | 676 | 17576 | 456976 | 11881376 | 308915776 | 132860 | 3454360 | 89813360 |
| 31 | 6860 | 961 | 29791 | 923521 | 28629151 | 887503681 | 212660 | 6592460 | 204366260 |
| 36 | 8820 | 1296 | 46656 | 1679616 | 60466176 | 2176782336 | 317520 | 11430720 | 411505920 |
| 41 | 9650 | 1681 | 68921 | 2825761 | 115856201 | 4750104241 | 395650 | 16221650 | 665087650 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| ∑x=189 | ∑y=47020 | ∑x2=5469 | ∑x3=177849 | ∑x4=6161829 | ∑x5=222134409 | ∑x6=8227667589 | ∑x·y=1267320 | ∑x2·y=41151620 | ∑x3·y=1433164920 |
Substituting these values in the normal equations
9a+189b+5469c+177849d=47020
189a+5469b+177849c+6161829d=1267320
5469a+177849b+6161829c+222134409d=41151620
177849a+6161829b+222134409c+8227667589d=1433164920
Solving these 4 equations,
Total Equations are 4
9a+189b+5469c+177849d=47020→(1)
189a+5469b+177849c+6161829d=1267320→(2)
5469a+177849b+6161829c+222134409d=41151620→(3)
177849a+6161829b+222134409c+8227667589d=1433164920→(4)
Select the equations (1) and (2), and eliminate the variable a.

Select the equations (1) and (3), and eliminate the variable a.

Select the equations (1) and (4), and eliminate the variable a.

Select the equations (5) and (6), and eliminate the variable b.

Select the equations (5) and (7), and eliminate the variable b.

Select the equations (8) and (9), and eliminate the variable c.

Now use back substitution method
From (10)
-22275000d=745500
⇒d=745500-22275000=-0.0335
From (8)
577500c+36382500d=2470000
⇒577500c+36382500(-0.0335)=2470000
⇒577500c-1217650=2470000
⇒577500c=2470000+1217650=3687650
⇒c=3687650577500=6.3855
From (5)
-1500b-63000c-2427000d=-279900
⇒-1500b-63000(6.3855)-2427000(-0.0335)=-279900
⇒-1500b-321062.2222=-279900
⇒-1500b=-279900+321062.2222=41162.2222
⇒b=41162.2222-1500=-27.4415
From (1)
9a+189b+5469c+177849d=47020
⇒9a+189(-27.4415)+5469(6.3855)+177849(-0.0335)=47020
⇒9a+23783.8317=47020
⇒9a=47020-23783.8317=23236.1683
⇒a=23236.16839=2581.7965
Solution using Elimination method.
a=2581.7965,b=-27.4415,c=6.3855,d=-0.0335
Now substituting this values in the equation is
Scatter graph of the model is given below.
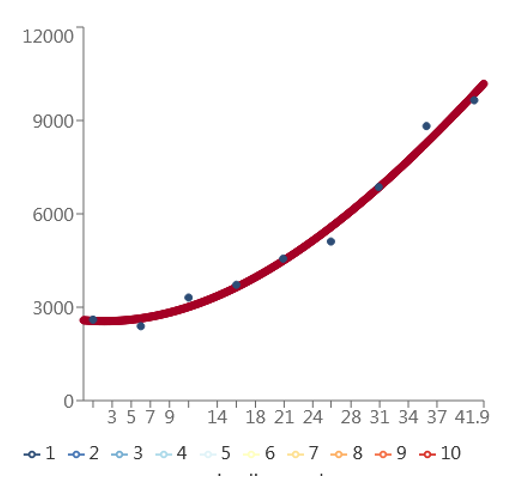
(c)
To find: The cost of tuition fee in 2021.
According to quadratic regression the cost of tuition fee in 2021 is 11849 .
According to cubic regression the cost of tuition fee in 2021 is 14082
Given informationquadratic regression is
Substitute x=46 in the above equation
Cubic equation model is
Now Substitute x=46 in the above equation
(d)
To find: The end behaviour of the model.
The model of the given data
Given information
According to quadratic model the future expense will not go too high. But the cubic model says otherwise. It predicts that future expanse will be very high.
Chapter 2 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
- Let y(t) represent your retirement account balance, in dollars, after t years. Each year the account earns 7% interest, and you deposit 8% of your annual income. Your current annual income is $34000, but it is growing at a continuous rate of 2% per year. Write the differential equation modeling this situation. dy dtarrow_forward8:37 ▬▬▬▬▬▬▬▬▬ Ο Graph of f The figure shows the graph of a periodic function f in the xy-plane. What is the frequency of f? 0.5 B 2 C 3 D 8 3 of 6 ^ Oli Back Next apclassroom.collegeboard.orgarrow_forward2. The growth of bacteria in food products makes it necessary to time-date some products (such as milk) so that they will be sold and consumed before the bacteria count is too high. Suppose for a certain product that the number of bacteria present is given by f(t)=5000.1 Under certain storage conditions, where t is time in days after packing of the product and the value of f(t) is in millions. The solution to word problems should always be given in a complete sentence, with appropriate units, in the context of the problem. (a) If the product cannot be safely eaten after the bacteria count reaches 3000 million, how long will this take? (b) If t=0 corresponds to January 1, what date should be placed on the product?arrow_forward
- 2.6 Applications: Growth and Decay; Mathematics of Finances 1. A couple wants to have $50,000 in 5 years for a down payment on a new house. (a) How much should they deposit today, at 6.2% compounded quarterly, to have the required amount in 5 years? (b) How much interest will be earned? (c) If they can deposit only $30,000 now, how much more will they need to complete the $50,000 after 5 years? Note, this is not 50,000-P3.arrow_forwardThe graph of f(x) is given below. Select each true statement about the continuity of f(x) at x = 1. Select all that apply: ☐ f(x) is not continuous at x = 1 because it is not defined at x = 1. ☐ f(x) is not continuous at x = 1 because lim f(x) does not exist. x+1 ☐ f(x) is not continuous at x = 1 because lim f(x) ‡ f(1). x+→1 ☐ f(x) is continuous at x = 1.arrow_forwarda is done please show barrow_forward
- A homeware company has been approached to manufacture a cake tin in the shape of a "ghost" from the Pac-Man video game to celebrate the 45th Anniversary of the games launch. The base of the cake tin has a characteristic dimension / and is illustrated in Figure 1 below, you should assume the top and bottom of the shape can be represented by semi-circles. The vertical sides of the cake tin have a height of h. As the company's resident mathematician, you need to find the values of r and h that minimise the internal surface area of the cake tin given that the volume of the tin is Vfixed- 2r Figure 1 - Plan view of the "ghost" cake tin base. (a) Show that the Volume (V) of the cake tin as a function of r and his 2(+1)²h V = 2arrow_forward15. Please solve this and show each and every step please. PLEASE no chatgpt can I have a real person solve it please!! I am stuck. I am doing pratice problems and I do not even know where to start with this. The question is Please compute the indicated functional value.arrow_forwardUse a graph of f to estimate lim f(x) or to show that the limit does not exist. Evaluate f(x) near x = a to support your conjecture. Complete parts (a) and (b). x-a f(x)= 1 - cos (4x-4) 3(x-1)² ; a = 1 a. Use a graphing utility to graph f. Select the correct graph below.. A. W → ✓ Each graph is displayed in a [- 1,3] by [0,5] window. B. in ✓ ○ C. und ☑ Use the graphing utility to estimate lim f(x). Select the correct choice below and, if necessary, fill in the answer box to complete your choice. x-1 ○ A. The limit appears to be approximately ☐ . (Round to the nearest tenth as needed.) B. The limit does not exist. b. Evaluate f(x) for values of x near 1 to support your conjecture. X 0.9 0.99 0.999 1.001 1.01 1.1 f(x) ○ D. + ☑ (Round to six decimal places as needed.) Does the table from the previous step support your conjecture? A. No, it does not. The function f(x) approaches a different value in the table of values than in the graph, after the approached values are rounded to the…arrow_forward
- x²-19x+90 Let f(x) = . Complete parts (a) through (c) below. x-a a. For what values of a, if any, does lim f(x) equal a finite number? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. x→a+ ○ A. a= (Type an integer or a simplified fraction. Use a comma to separate answers as needed.) B. There are no values of a for which the limit equals a finite number. b. For what values of a, if any, does lim f(x) = ∞o? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. x→a+ A. (Type integers or simplified fractions) C. There are no values of a that satisfy lim f(x) = ∞. + x-a c. For what values of a, if any, does lim f(x) = -∞0? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. x→a+ A. Either a (Type integers or simplified fractions) B.arrow_forwardSketch a possible graph of a function f, together with vertical asymptotes, that satisfies all of the following conditions. f(2)=0 f(4) is undefined lim f(x)=1 X-6 lim f(x) = -∞ x-0+ lim f(x) = ∞ lim f(x) = ∞ x-4 _8arrow_forwardDetermine the following limit. lim 35w² +8w+4 w→∞ √49w+w³ 3 Select the correct choice below, and, if necessary, fill in the answer box to complete your choice. ○ A. lim W→∞ 35w² +8w+4 49w+w3 (Simplify your answer.) B. The limit does not exist and is neither ∞ nor - ∞.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning