(a).

To find: The real values of x that cause the function to be zero.

The real value of x is equal to −5 .

Given information:

Consider the given function.

fx=x+52x+1x−1

Calculation:

When the given function fx is zero, then the values of x can be calculated as follow:

x+5=0x+5=0x=−5

Thus, the real values of x are equal to −5 .

(b).

To find: The real values of x that cause the function to be undefined.

The real values of x are equal to −12,1 .

Given information:

Consider the given function.

fx=x+52x+1x−1

Calculation:

When the given function fx is undefined, then substitute the denominator equal to zero and calculate the values of x below:

2x+1x−1=02x+1=02x=−1x=−12

And

2x+1x−1=0x−1=0x=1

Therefore, the real values of x are −12,1 for the function fx is undefined.

(c).

To find: The real values of x that cause the function to be positive.

The real values of x is equal to −5,−12∪1,∞ .

Given information:

Consider the given function.

fx=x+52x+1x−1

Calculation:

The given function fx is positive.

First find the boundary points of the function fx .

Substitute the numerator and the denominator equal to zero, then calculate the values of x below:

x+5=0x+5=0x=−5

And

2x+1x−1=0x=−12,1

So, the boundary points of the function fx are −5,−12,1 .

Now, locate these boundary points on the number line (or sign chart) and dividing the number line into intervals and check the function fx is positive or negative at each interval below:

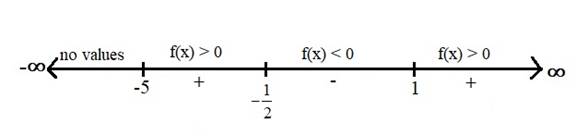
Therefore, the given function fx is positive into −5,−12∪1,∞ .

Hence, the real values of x is equal to −5,−12∪1,∞ .

(d).

To find: The real values of x that cause the function to be negative.

The real values of x is equal to −12,1 .

Given information:

Consider the given function.

fx=x+52x+1x−1

Calculation:

The given function fx is negative.

First find the boundary points of the function fx .

Substitute the numerator and the denominator equal to zero, then calculate the values of x below:

x+5=0x+5=0x=−5

And

2x+1x−1=0x=−12,1

So, the boundary points of the function fx are −5,−12,1 .

Now, locate these boundary points on the number line (or sign chart) and dividing the number line into intervals and check the function fx is positive or negative at each interval below:

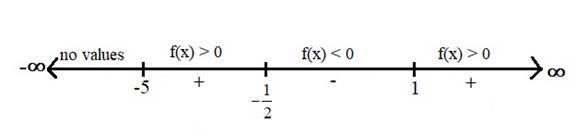
Therefore, the given function fx is negative into −12,1 .

Hence, the real values of x is equal to −12,1 .

Chapter 2.8, Problem 28E

Chapter 2.8, Problem 30E

Chapter 2 Solutions

PRECALCULUS:GRAPHICAL,...-NASTA ED.

Ch. 2.1 - Prob. 1QR Ch. 2.1 - Prob. 2QR Ch. 2.1 - Prob. 3QR Ch. 2.1 - Prob. 4QR Ch. 2.1 - Prob. 5QR Ch. 2.1 - Prob. 6QR Ch. 2.1 - Prob. 7QR Ch. 2.1 - Prob. 8QR Ch. 2.1 - Prob. 9QR Ch. 2.1 - Prob. 10QR

Ch. 2.1 - Prob. 1E Ch. 2.1 - Prob. 2E Ch. 2.1 - Prob. 3E Ch. 2.1 - Prob. 4E Ch. 2.1 - Prob. 5E Ch. 2.1 - Prob. 6E Ch. 2.1 - Prob. 7E Ch. 2.1 - Prob. 8E Ch. 2.1 - Prob. 9E Ch. 2.1 - Prob. 10E Ch. 2.1 - Prob. 11E Ch. 2.1 - Prob. 12E Ch. 2.1 - Prob. 13E Ch. 2.1 - Prob. 14E Ch. 2.1 - Prob. 15E Ch. 2.1 - Prob. 16E Ch. 2.1 - Prob. 17E Ch. 2.1 - Prob. 18E Ch. 2.1 - Prob. 19E Ch. 2.1 - Prob. 20E Ch. 2.1 - Prob. 21E Ch. 2.1 - Prob. 22E Ch. 2.1 - Prob. 23E Ch. 2.1 - Prob. 24E Ch. 2.1 - Prob. 25E Ch. 2.1 - Prob. 26E Ch. 2.1 - Prob. 27E Ch. 2.1 - Prob. 28E Ch. 2.1 - Prob. 29E Ch. 2.1 - Prob. 30E Ch. 2.1 - Prob. 31E Ch. 2.1 - Prob. 32E Ch. 2.1 - Prob. 33E Ch. 2.1 - Prob. 34E Ch. 2.1 - Prob. 35E Ch. 2.1 - Prob. 36E Ch. 2.1 - Prob. 37E Ch. 2.1 - Prob. 38E Ch. 2.1 - Prob. 39E Ch. 2.1 - Prob. 40E Ch. 2.1 - Prob. 41E Ch. 2.1 - Prob. 42E Ch. 2.1 - Prob. 43E Ch. 2.1 - Prob. 44E Ch. 2.1 - Prob. 45E Ch. 2.1 - Prob. 46E Ch. 2.1 - Prob. 47E Ch. 2.1 - Prob. 48E Ch. 2.1 - Prob. 49E Ch. 2.1 - Prob. 50E Ch. 2.1 - Prob. 51E Ch. 2.1 - Prob. 52E Ch. 2.1 - Prob. 53E Ch. 2.1 - Prob. 54E Ch. 2.1 - Prob. 55E Ch. 2.1 - Prob. 56E Ch. 2.1 - Prob. 57E Ch. 2.1 - Prob. 58E Ch. 2.1 - Prob. 59E Ch. 2.1 - Prob. 60E Ch. 2.1 - Prob. 61E Ch. 2.1 - Prob. 62E Ch. 2.1 - Prob. 63E Ch. 2.1 - Prob. 64E Ch. 2.1 - Prob. 65E Ch. 2.1 - Prob. 66E Ch. 2.1 - Prob. 67E Ch. 2.1 - Prob. 68E Ch. 2.1 - Prob. 69E Ch. 2.1 - Prob. 70E Ch. 2.1 - Prob. 71E Ch. 2.1 - Prob. 72E Ch. 2.1 - Prob. 73E Ch. 2.1 - Prob. 74E Ch. 2.1 - Prob. 75E Ch. 2.1 - Prob. 76E Ch. 2.1 - Prob. 77E Ch. 2.1 - Prob. 78E Ch. 2.1 - Prob. 79E Ch. 2.1 - Prob. 80E Ch. 2.1 - Prob. 81E Ch. 2.1 - Prob. 82E Ch. 2.1 - Prob. 84E Ch. 2.1 - Prob. 85E Ch. 2.1 - Prob. 86E Ch. 2.1 - Prob. 87E Ch. 2.1 - Prob. 88E Ch. 2.1 - Prob. 89E Ch. 2.2 - Prob. 1QR Ch. 2.2 - Prob. 2QR Ch. 2.2 - Prob. 3QR Ch. 2.2 - Prob. 4QR Ch. 2.2 - Prob. 5QR Ch. 2.2 - Prob. 6QR Ch. 2.2 - Prob. 7QR Ch. 2.2 - Prob. 8QR Ch. 2.2 - Prob. 9QR Ch. 2.2 - Prob. 10QR Ch. 2.2 - Prob. 1E Ch. 2.2 - Prob. 2E Ch. 2.2 - Prob. 3E Ch. 2.2 - Prob. 4E Ch. 2.2 - Prob. 5E Ch. 2.2 - Prob. 6E Ch. 2.2 - Prob. 7E Ch. 2.2 - Prob. 8E Ch. 2.2 - Prob. 9E Ch. 2.2 - Prob. 10E Ch. 2.2 - Prob. 11E Ch. 2.2 - Prob. 12E Ch. 2.2 - Prob. 13E Ch. 2.2 - Prob. 14E Ch. 2.2 - Prob. 15E Ch. 2.2 - Prob. 16E Ch. 2.2 - Prob. 17E Ch. 2.2 - Prob. 18E Ch. 2.2 - Prob. 19E Ch. 2.2 - Prob. 20E Ch. 2.2 - Prob. 21E Ch. 2.2 - Prob. 22E Ch. 2.2 - Prob. 23E Ch. 2.2 - Prob. 24E Ch. 2.2 - Prob. 25E Ch. 2.2 - Prob. 26E Ch. 2.2 - Prob. 27E Ch. 2.2 - Prob. 28E Ch. 2.2 - Prob. 29E Ch. 2.2 - Prob. 30E Ch. 2.2 - Prob. 31E Ch. 2.2 - Prob. 32E Ch. 2.2 - Prob. 33E Ch. 2.2 - Prob. 34E Ch. 2.2 - Prob. 35E Ch. 2.2 - Prob. 36E Ch. 2.2 - Prob. 37E Ch. 2.2 - Prob. 38E Ch. 2.2 - Prob. 39E Ch. 2.2 - Prob. 40E Ch. 2.2 - Prob. 41E Ch. 2.2 - Prob. 42E Ch. 2.2 - Prob. 43E Ch. 2.2 - Prob. 44E Ch. 2.2 - Prob. 45E Ch. 2.2 - Prob. 46E Ch. 2.2 - Prob. 47E Ch. 2.2 - Prob. 48E Ch. 2.2 - Prob. 49E Ch. 2.2 - Prob. 50E Ch. 2.2 - Prob. 51E Ch. 2.2 - Prob. 52E Ch. 2.2 - Prob. 53E Ch. 2.2 - Prob. 54E Ch. 2.2 - Prob. 55E Ch. 2.2 - Prob. 56E Ch. 2.2 - Prob. 57E Ch. 2.2 - Prob. 58E Ch. 2.2 - Prob. 59E Ch. 2.2 - Prob. 60E Ch. 2.2 - Prob. 61E Ch. 2.2 - Prob. 62E Ch. 2.2 - Prob. 63E Ch. 2.2 - Prob. 65E Ch. 2.2 - Prob. 66E Ch. 2.2 - Prob. 67E Ch. 2.2 - Prob. 68E Ch. 2.2 - Prob. 69E Ch. 2.2 - Prob. 70E Ch. 2.2 - Prob. 71E Ch. 2.3 - Prob. 1QR Ch. 2.3 - Prob. 2QR Ch. 2.3 - Prob. 3QR Ch. 2.3 - Prob. 4QR Ch. 2.3 - Prob. 5QR Ch. 2.3 - Prob. 6QR Ch. 2.3 - Prob. 7QR Ch. 2.3 - Prob. 8QR Ch. 2.3 - Prob. 9QR Ch. 2.3 - Prob. 10QR Ch. 2.3 - Prob. 1E Ch. 2.3 - Prob. 2E Ch. 2.3 - Prob. 3E Ch. 2.3 - Prob. 4E Ch. 2.3 - Prob. 5E Ch. 2.3 - Prob. 6E Ch. 2.3 - Prob. 7E Ch. 2.3 - Prob. 8E Ch. 2.3 - Prob. 9E Ch. 2.3 - Prob. 10E Ch. 2.3 - Prob. 11E Ch. 2.3 - Prob. 12E Ch. 2.3 - Prob. 13E Ch. 2.3 - Prob. 14E Ch. 2.3 - Prob. 15E Ch. 2.3 - Prob. 16E Ch. 2.3 - Prob. 17E Ch. 2.3 - Prob. 18E Ch. 2.3 - Prob. 19E Ch. 2.3 - Prob. 20E Ch. 2.3 - Prob. 21E Ch. 2.3 - Prob. 22E Ch. 2.3 - Prob. 23E Ch. 2.3 - Prob. 24E Ch. 2.3 - Prob. 25E Ch. 2.3 - Prob. 26E Ch. 2.3 - Prob. 27E Ch. 2.3 - Prob. 28E Ch. 2.3 - Prob. 29E Ch. 2.3 - Prob. 30E Ch. 2.3 - Prob. 31E Ch. 2.3 - Prob. 32E Ch. 2.3 - Prob. 33E Ch. 2.3 - Prob. 34E Ch. 2.3 - In Exercises 3338, find the zeros of the function...Ch. 2.3 - Prob. 36E Ch. 2.3 - Prob. 37E Ch. 2.3 - Prob. 38E Ch. 2.3 - Prob. 39E Ch. 2.3 - Prob. 40E Ch. 2.3 - Prob. 41E Ch. 2.3 - Prob. 42E Ch. 2.3 - Prob. 43E Ch. 2.3 - Prob. 44E Ch. 2.3 - Prob. 45E Ch. 2.3 - Prob. 46E Ch. 2.3 - Prob. 47E Ch. 2.3 - Prob. 48E Ch. 2.3 - Prob. 49E Ch. 2.3 - Prob. 50E Ch. 2.3 - Prob. 51E Ch. 2.3 - Prob. 52E Ch. 2.3 - Prob. 53E Ch. 2.3 - Prob. 54E Ch. 2.3 - Prob. 55E Ch. 2.3 - Prob. 56E Ch. 2.3 - Prob. 57E Ch. 2.3 - Prob. 58E Ch. 2.3 - Prob. 59E Ch. 2.3 - Prob. 60E Ch. 2.3 - Prob. 61E Ch. 2.3 - Prob. 62E Ch. 2.3 - Prob. 63E Ch. 2.3 - Prob. 64E Ch. 2.3 - Prob. 65E Ch. 2.3 - Prob. 66E Ch. 2.3 - Prob. 67E Ch. 2.3 - Prob. 68E Ch. 2.3 - Prob. 69E Ch. 2.3 - Prob. 70E Ch. 2.3 - Prob. 71E Ch. 2.3 - Prob. 72E Ch. 2.3 - Prob. 73E Ch. 2.3 - Prob. 74E Ch. 2.3 - Prob. 75E Ch. 2.3 - Prob. 76E Ch. 2.3 - Prob. 77E Ch. 2.3 - Prob. 78E Ch. 2.3 - Prob. 79E Ch. 2.3 - Prob. 80E Ch. 2.3 - Prob. 81E Ch. 2.3 - Prob. 82E Ch. 2.3 - Prob. 83E Ch. 2.3 - Prob. 84E Ch. 2.3 - Prob. 85E Ch. 2.4 - Prob. 1QR Ch. 2.4 - Prob. 2QR Ch. 2.4 - Prob. 3QR Ch. 2.4 - Prob. 4QR Ch. 2.4 - Prob. 5QR Ch. 2.4 - Prob. 6QR Ch. 2.4 - Prob. 7QR Ch. 2.4 - Prob. 8QR Ch. 2.4 - Prob. 9QR Ch. 2.4 - Prob. 10QR Ch. 2.4 - Prob. 1E Ch. 2.4 - Prob. 2E Ch. 2.4 - Prob. 3E Ch. 2.4 - Prob. 4E Ch. 2.4 - Prob. 5E Ch. 2.4 - Prob. 6E Ch. 2.4 - Prob. 7E Ch. 2.4 - Prob. 8E Ch. 2.4 - Prob. 9E Ch. 2.4 - Prob. 10E Ch. 2.4 - Prob. 11E Ch. 2.4 - Prob. 12E Ch. 2.4 - Prob. 13E Ch. 2.4 - Prob. 14E Ch. 2.4 - Prob. 15E Ch. 2.4 - Prob. 16E Ch. 2.4 - Prob. 17E Ch. 2.4 - Prob. 18E Ch. 2.4 - Prob. 19E Ch. 2.4 - Prob. 20E Ch. 2.4 - Prob. 21E Ch. 2.4 - Prob. 22E Ch. 2.4 - Prob. 23E Ch. 2.4 - Prob. 24E Ch. 2.4 - Prob. 25E Ch. 2.4 - Prob. 26E Ch. 2.4 - Prob. 27E Ch. 2.4 - Prob. 28E Ch. 2.4 - Prob. 29E Ch. 2.4 - Prob. 30E Ch. 2.4 - Prob. 31E Ch. 2.4 - Prob. 32E Ch. 2.4 - Prob. 33E Ch. 2.4 - Prob. 34E Ch. 2.4 - Prob. 35E Ch. 2.4 - Prob. 36E Ch. 2.4 - Prob. 37E Ch. 2.4 - Prob. 38E Ch. 2.4 - Prob. 39E Ch. 2.4 - Prob. 40E Ch. 2.4 - Prob. 41E Ch. 2.4 - Prob. 42E Ch. 2.4 - Prob. 43E Ch. 2.4 - Prob. 44E Ch. 2.4 - Prob. 45E Ch. 2.4 - Prob. 46E Ch. 2.4 - Prob. 47E Ch. 2.4 - Prob. 48E Ch. 2.4 - Prob. 49E Ch. 2.4 - Prob. 50E Ch. 2.4 - Prob. 51E Ch. 2.4 - Prob. 52E Ch. 2.4 - Prob. 53E Ch. 2.4 - Prob. 54E Ch. 2.4 - Prob. 55E Ch. 2.4 - Prob. 56E Ch. 2.4 - Prob. 57E Ch. 2.4 - Prob. 58E Ch. 2.4 - Prob. 59E Ch. 2.4 - Prob. 60E Ch. 2.4 - Prob. 61E Ch. 2.4 - Prob. 62E Ch. 2.4 - Prob. 63E Ch. 2.4 - Prob. 64E Ch. 2.4 - Prob. 65E Ch. 2.4 - Prob. 66E Ch. 2.4 - Prob. 67E Ch. 2.4 - Prob. 68E Ch. 2.4 - Prob. 69E Ch. 2.4 - Prob. 70E Ch. 2.4 - Prob. 71E Ch. 2.4 - Prob. 72E Ch. 2.4 - Prob. 73E Ch. 2.4 - Prob. 74E Ch. 2.4 - Prob. 75E Ch. 2.4 - Prob. 76E Ch. 2.4 - Prob. 77E Ch. 2.4 - Prob. 78E Ch. 2.4 - Prob. 79E Ch. 2.5 - Prob. 1QR Ch. 2.5 - Prob. 2QR Ch. 2.5 - Prob. 3QR Ch. 2.5 - Prob. 4QR Ch. 2.5 - Prob. 5QR Ch. 2.5 - Prob. 6QR Ch. 2.5 - Prob. 7QR Ch. 2.5 - Prob. 8QR Ch. 2.5 - Prob. 9QR Ch. 2.5 - Prob. 10QR Ch. 2.5 - Prob. 1E Ch. 2.5 - Prob. 2E Ch. 2.5 - Prob. 3E Ch. 2.5 - Prob. 4E Ch. 2.5 - Prob. 5E Ch. 2.5 - Prob. 6E Ch. 2.5 - Prob. 7E Ch. 2.5 - Prob. 8E Ch. 2.5 - Prob. 9E Ch. 2.5 - Prob. 10E Ch. 2.5 - Prob. 11E Ch. 2.5 - Prob. 12E Ch. 2.5 - Prob. 13E Ch. 2.5 - Prob. 14E Ch. 2.5 - Prob. 15E Ch. 2.5 - Prob. 16E Ch. 2.5 - Prob. 17E Ch. 2.5 - Prob. 18E Ch. 2.5 - Prob. 19E Ch. 2.5 - Prob. 20E Ch. 2.5 - Prob. 21E Ch. 2.5 - Prob. 22E Ch. 2.5 - Prob. 23E Ch. 2.5 - Prob. 24E Ch. 2.5 - Prob. 25E Ch. 2.5 - Prob. 26E Ch. 2.5 - Prob. 27E Ch. 2.5 - Prob. 28E Ch. 2.5 - In Exercises 2732, find all of the zeros and write...Ch. 2.5 - In Exercises 2732, find all of the zeros and write...Ch. 2.5 - Prob. 31E Ch. 2.5 - Prob. 32E Ch. 2.5 - Prob. 33E Ch. 2.5 - Prob. 34E Ch. 2.5 - Prob. 35E Ch. 2.5 - Prob. 36E Ch. 2.5 - Prob. 37E Ch. 2.5 - Prob. 38E Ch. 2.5 - Prob. 39E Ch. 2.5 - Prob. 40E Ch. 2.5 - Prob. 41E Ch. 2.5 - Prob. 42E Ch. 2.5 - Prob. 43E Ch. 2.5 - Prob. 44E Ch. 2.5 - Prob. 45E Ch. 2.5 - Prob. 46E Ch. 2.5 - Prob. 47E Ch. 2.5 - Prob. 48E Ch. 2.5 - Prob. 49E Ch. 2.5 - Prob. 50E Ch. 2.5 - Prob. 51E Ch. 2.5 - Prob. 52E Ch. 2.5 - Prob. 53E Ch. 2.5 - Prob. 54E Ch. 2.5 - Prob. 55E Ch. 2.5 - Prob. 56E Ch. 2.5 - Prob. 57E Ch. 2.5 - Prob. 58E Ch. 2.5 - Prob. 60E Ch. 2.5 - Prob. 61E Ch. 2.5 - Prob. 62E Ch. 2.5 - Prob. 63E Ch. 2.5 - Prob. 64E Ch. 2.5 - Prob. 65E Ch. 2.5 - Prob. 66E Ch. 2.6 - Prob. 1QR Ch. 2.6 - Prob. 2QR Ch. 2.6 - Prob. 3QR Ch. 2.6 - Prob. 4QR Ch. 2.6 - Prob. 5QR Ch. 2.6 - Prob. 6QR Ch. 2.6 - Prob. 7QR Ch. 2.6 - Prob. 8QR Ch. 2.6 - Prob. 9QR Ch. 2.6 - Prob. 10QR Ch. 2.6 - Prob. 1E Ch. 2.6 - Prob. 2E Ch. 2.6 - Prob. 3E Ch. 2.6 - Prob. 4E Ch. 2.6 - Prob. 5E Ch. 2.6 - Prob. 6E Ch. 2.6 - Prob. 7E Ch. 2.6 - Prob. 8E Ch. 2.6 - Prob. 9E Ch. 2.6 - Prob. 10E Ch. 2.6 - Prob. 11E Ch. 2.6 - Prob. 12E Ch. 2.6 - Prob. 13E Ch. 2.6 - Prob. 14E Ch. 2.6 - Prob. 15E Ch. 2.6 - Prob. 16E Ch. 2.6 - Prob. 17E Ch. 2.6 - Prob. 18E Ch. 2.6 - Prob. 19E Ch. 2.6 - Prob. 20E Ch. 2.6 - Prob. 21E Ch. 2.6 - Prob. 22E Ch. 2.6 - Prob. 23E Ch. 2.6 - Prob. 24E Ch. 2.6 - Prob. 25E Ch. 2.6 - Prob. 26E Ch. 2.6 - Prob. 27E Ch. 2.6 - Prob. 28E Ch. 2.6 - Prob. 29E Ch. 2.6 - Prob. 30E Ch. 2.6 - Prob. 31E Ch. 2.6 - Prob. 32E Ch. 2.6 - Prob. 33E Ch. 2.6 - Prob. 34E Ch. 2.6 - Prob. 35E Ch. 2.6 - Prob. 36E Ch. 2.6 - Prob. 37E Ch. 2.6 - Prob. 38E Ch. 2.6 - Prob. 39E Ch. 2.6 - Prob. 40E Ch. 2.6 - Prob. 41E Ch. 2.6 - Prob. 42E Ch. 2.6 - Prob. 43E Ch. 2.6 - Prob. 44E Ch. 2.6 - In Exercises 4550, find the end behavior asymptote...Ch. 2.6 - Prob. 46E Ch. 2.6 - Prob. 47E Ch. 2.6 - Prob. 48E Ch. 2.6 - Prob. 49E Ch. 2.6 - Prob. 50E Ch. 2.6 - Prob. 51E Ch. 2.6 - Prob. 52E Ch. 2.6 - Prob. 53E Ch. 2.6 - Prob. 54E Ch. 2.6 - Prob. 55E Ch. 2.6 - Prob. 56E Ch. 2.6 - Prob. 57E Ch. 2.6 - Prob. 58E Ch. 2.6 - Prob. 59E Ch. 2.6 - Prob. 60E Ch. 2.6 - Prob. 61E Ch. 2.6 - Prob. 62E Ch. 2.6 - Prob. 63E Ch. 2.6 - Prob. 64E Ch. 2.6 - Prob. 65E Ch. 2.6 - Prob. 66E Ch. 2.6 - Prob. 67E Ch. 2.6 - Prob. 68E Ch. 2.6 - Prob. 69E Ch. 2.6 - Prob. 70E Ch. 2.6 - Prob. 71E Ch. 2.6 - Prob. 72E Ch. 2.6 - Prob. 73E Ch. 2.6 - Prob. 74E Ch. 2.6 - Prob. 75E Ch. 2.6 - Prob. 76E Ch. 2.6 - Prob. 77E Ch. 2.6 - Prob. 78E Ch. 2.6 - Prob. 79E Ch. 2.6 - Prob. 80E Ch. 2.6 - Prob. 81E Ch. 2.6 - Prob. 82E Ch. 2.7 - Prob. 1QR Ch. 2.7 - Prob. 2QR Ch. 2.7 - Prob. 3QR Ch. 2.7 - Prob. 4QR Ch. 2.7 - Prob. 5QR Ch. 2.7 - Prob. 6QR Ch. 2.7 - Prob. 7QR Ch. 2.7 - Prob. 8QR Ch. 2.7 - Prob. 9QR Ch. 2.7 - Prob. 10QR Ch. 2.7 - Prob. 1E Ch. 2.7 - Prob. 2E Ch. 2.7 - Prob. 3E Ch. 2.7 - Prob. 4E Ch. 2.7 - Prob. 5E Ch. 2.7 - Prob. 6E Ch. 2.7 - Prob. 7E Ch. 2.7 - Prob. 8E Ch. 2.7 - Prob. 9E Ch. 2.7 - Prob. 10E Ch. 2.7 - Prob. 11E Ch. 2.7 - Prob. 12E Ch. 2.7 - Prob. 13E Ch. 2.7 - Prob. 14E Ch. 2.7 - Prob. 15E Ch. 2.7 - Prob. 16E Ch. 2.7 - Prob. 17E Ch. 2.7 - Prob. 18E Ch. 2.7 - Prob. 19E Ch. 2.7 - Prob. 20E Ch. 2.7 - Prob. 21E Ch. 2.7 - Prob. 22E Ch. 2.7 - Prob. 23E Ch. 2.7 - Prob. 24E Ch. 2.7 - Prob. 25E Ch. 2.7 - Prob. 26E Ch. 2.7 - Prob. 27E Ch. 2.7 - Prob. 28E Ch. 2.7 - Prob. 29E Ch. 2.7 - Prob. 30E Ch. 2.7 - Prob. 31E Ch. 2.7 - Prob. 32E Ch. 2.7 - Prob. 33E Ch. 2.7 - Prob. 34E Ch. 2.7 - Prob. 35E Ch. 2.7 - Prob. 36E Ch. 2.7 - Prob. 37E Ch. 2.7 - Prob. 38E Ch. 2.7 - Prob. 39E Ch. 2.7 - Prob. 40E Ch. 2.7 - Prob. 41E Ch. 2.7 - Prob. 42E Ch. 2.7 - Prob. 43E Ch. 2.7 - Prob. 44E Ch. 2.7 - Prob. 45E Ch. 2.7 - Prob. 46E Ch. 2.7 - Prob. 47E Ch. 2.7 - Prob. 48E Ch. 2.7 - Prob. 49E Ch. 2.7 - Prob. 50E Ch. 2.7 - Prob. 51E Ch. 2.7 - Prob. 52E Ch. 2.7 - Prob. 53E Ch. 2.7 - Prob. 54E Ch. 2.7 - Prob. 55E Ch. 2.8 - Prob. 1QR Ch. 2.8 - Prob. 2QR Ch. 2.8 - Prob. 3QR Ch. 2.8 - Prob. 4QR Ch. 2.8 - Prob. 5QR Ch. 2.8 - Prob. 6QR Ch. 2.8 - Prob. 7QR Ch. 2.8 - Prob. 8QR Ch. 2.8 - Prob. 9QR Ch. 2.8 - Prob. 10QR Ch. 2.8 - Prob. 1E Ch. 2.8 - Prob. 2E Ch. 2.8 - Prob. 3E Ch. 2.8 - Prob. 4E Ch. 2.8 - Prob. 5E Ch. 2.8 - Prob. 6E Ch. 2.8 - Prob. 7E Ch. 2.8 - Prob. 8E Ch. 2.8 - Prob. 9E Ch. 2.8 - Prob. 10E Ch. 2.8 - Prob. 11E Ch. 2.8 - Prob. 12E Ch. 2.8 - Prob. 13E Ch. 2.8 - Prob. 14E Ch. 2.8 - Prob. 15E Ch. 2.8 - Prob. 16E Ch. 2.8 - Prob. 17E Ch. 2.8 - Prob. 18E Ch. 2.8 - Prob. 19E Ch. 2.8 - Prob. 20E Ch. 2.8 - Prob. 21E Ch. 2.8 - Prob. 22E Ch. 2.8 - Prob. 23E Ch. 2.8 - Prob. 24E Ch. 2.8 - Prob. 25E Ch. 2.8 - Prob. 26E Ch. 2.8 - Prob. 27E Ch. 2.8 - Prob. 28E Ch. 2.8 - Prob. 29E Ch. 2.8 - Prob. 30E Ch. 2.8 - Prob. 31E Ch. 2.8 - Prob. 32E Ch. 2.8 - Prob. 33E Ch. 2.8 - Prob. 34E Ch. 2.8 - Prob. 35E Ch. 2.8 - Prob. 36E Ch. 2.8 - Prob. 37E Ch. 2.8 - Prob. 38E Ch. 2.8 - Prob. 39E Ch. 2.8 - Prob. 40E Ch. 2.8 - Prob. 41E Ch. 2.8 - Prob. 42E Ch. 2.8 - Prob. 43E Ch. 2.8 - Prob. 44E Ch. 2.8 - Prob. 45E Ch. 2.8 - Prob. 46E Ch. 2.8 - Prob. 47E Ch. 2.8 - Prob. 48E Ch. 2.8 - Prob. 49E Ch. 2.8 - Prob. 50E Ch. 2.8 - Prob. 51E Ch. 2.8 - Prob. 52E Ch. 2.8 - Prob. 53E Ch. 2.8 - Prob. 54E Ch. 2.8 - Prob. 55E Ch. 2.8 - Prob. 56E Ch. 2.8 - Prob. 57E Ch. 2.8 - Prob. 58E Ch. 2.8 - Prob. 59E Ch. 2.8 - Prob. 60E Ch. 2.8 - Prob. 61E Ch. 2.8 - Prob. 62E Ch. 2.8 - Prob. 63E Ch. 2.8 - Prob. 64E Ch. 2.8 - Prob. 65E Ch. 2.8 - Prob. 66E Ch. 2.8 - Prob. 67E Ch. 2.8 - Prob. 68E Ch. 2.8 - Prob. 69E Ch. 2.8 - Prob. 70E Ch. 2.8 - Prob. 71E Ch. 2.8 - Prob. 72E Ch. 2.8 - Prob. 75E Ch. 2.8 - Prob. 76E Ch. 2 - Prob. 1RE Ch. 2 - Prob. 2RE Ch. 2 - Prob. 3RE Ch. 2 - Prob. 4RE Ch. 2 - Prob. 5RE Ch. 2 - Prob. 6RE Ch. 2 - Prob. 7RE Ch. 2 - Prob. 8RE Ch. 2 - Prob. 9RE Ch. 2 - Prob. 10RE Ch. 2 - Prob. 11RE Ch. 2 - Prob. 12RE Ch. 2 - Prob. 13RE Ch. 2 - Prob. 14RE Ch. 2 - Prob. 15RE Ch. 2 - Prob. 16RE Ch. 2 - Prob. 17RE Ch. 2 - Prob. 18RE Ch. 2 - Prob. 19RE Ch. 2 - Prob. 20RE Ch. 2 - Prob. 21RE Ch. 2 - Prob. 22RE Ch. 2 - Prob. 23RE Ch. 2 - Prob. 24RE Ch. 2 - Prob. 25RE Ch. 2 - Prob. 26RE Ch. 2 - Prob. 27RE Ch. 2 - Prob. 28RE Ch. 2 - Prob. 29RE Ch. 2 - Prob. 30RE Ch. 2 - Prob. 31RE Ch. 2 - Prob. 32RE Ch. 2 - Prob. 33RE Ch. 2 - Prob. 34RE Ch. 2 - Prob. 35RE Ch. 2 - Prob. 36RE Ch. 2 - Prob. 37RE Ch. 2 - Prob. 38RE Ch. 2 - Prob. 39RE Ch. 2 - Prob. 40RE Ch. 2 - Prob. 41RE Ch. 2 - Prob. 42RE Ch. 2 - Prob. 43RE Ch. 2 - Prob. 44RE Ch. 2 - Prob. 45RE Ch. 2 - Prob. 46RE Ch. 2 - Prob. 47RE Ch. 2 - Prob. 48RE Ch. 2 - Prob. 49RE Ch. 2 - Prob. 50RE Ch. 2 - Prob. 51RE Ch. 2 - Prob. 52RE Ch. 2 - Prob. 53RE Ch. 2 - Prob. 54RE Ch. 2 - Prob. 55RE Ch. 2 - Prob. 56RE Ch. 2 - Prob. 57RE Ch. 2 - Prob. 58RE Ch. 2 - Prob. 59RE Ch. 2 - Prob. 60RE Ch. 2 - Prob. 61RE Ch. 2 - Prob. 62RE Ch. 2 - Prob. 63RE Ch. 2 - Prob. 64RE Ch. 2 - Prob. 65RE Ch. 2 - Prob. 66RE Ch. 2 - Prob. 67RE Ch. 2 - Prob. 68RE Ch. 2 - Prob. 69RE Ch. 2 - Prob. 70RE Ch. 2 - Prob. 71RE Ch. 2 - Prob. 72RE Ch. 2 - Prob. 73RE Ch. 2 - Prob. 74RE Ch. 2 - Prob. 75RE Ch. 2 - Prob. 76RE Ch. 2 - Prob. 77RE Ch. 2 - Prob. 78RE Ch. 2 - Prob. 79RE Ch. 2 - Prob. 80RE Ch. 2 - Prob. 81RE Ch. 2 - Prob. 82RE Ch. 2 - Prob. 83RE Ch. 2 - Prob. 84RE Ch. 2 - Prob. 85RE Ch. 2 - Prob. 86RE Ch. 2 - Prob. 87RE Ch. 2 - Prob. 88RE Ch. 2 - Prob. 89RE Ch. 2 - Prob. 90RE Ch. 2 - Prob. 91RE Ch. 2 - Prob. 92RE Ch. 2 - Prob. 93RE Ch. 2 - Prob. 94RE Ch. 2 - Prob. 95RE Ch. 2 - Prob. 96RE Ch. 2 - Prob. 97RE Ch. 2 - Prob. 98RE Ch. 2 - Prob. 99RE

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning