
Concept explainers
The complete analysis of given function.
Domain:
Range:
Continuity:
Increasing-decreasing behaviour: The graph is always increasing.
Symmetry: The function is odd, so, the graph is symmetric about the origin.
Boundedness: Upper and lower bound
Local extrema: No Local Extrema
Horizontal asymptotes: No Asymptotes
Vertical asymptotes: No Asymptotes
End behaviour: Th graph falls to the left and rises to the right
Given:
Graph:
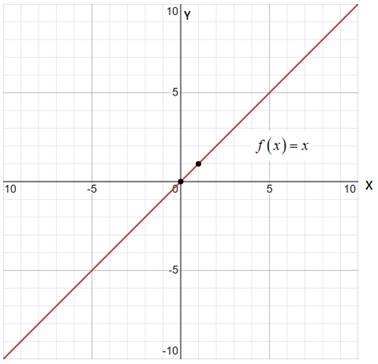
Domain:
The domain of the expression is all real numbers except where the expression is undefined. In this case, there is no real number that makes the expression undefined.
Interval Notation:
Set-Builder Notation:
Range:
The range is the set of all valid
Interval Notation:
Set-Builder Notation:
Continuity:
Since the domain is all real numbers,
Increasing-decreasing behaviour:
The function
Symmetry:
To determine if the function is odd, even, or neither in order to find the symmetry.
If the function is odd, the function is symmetric about the origin. And ff the function is even, the function is symmetric about the y-axis.
Find
A function is even if
Check if
Since
The function is not even.
A function is odd if
Multiply
Since
The function is odd.
Since the function is odd, the graph is symmetric about the origin.
Boundedness:
Find every combination of
If a polynomial function has integer coefficients, then every rational zero will have the form
Find every combination of
Apply synthetic division on
Since
Upper and lower bound:
Local extrema:
Differentiate
Since
To find the local maximum and minimum values of the function, set the derivative equal to
Since there is no value of
Horizontal asymptotes:
Since
Vertical asymptotes:
Since
End behaviour:
The largest exponent is the degree of the polynomial is
Since the degree is odd, the ends of the function will point in the opposite directions. Falls to the left and rises to the right
Since the leading coefficient is positive, the graph rises to the right.
From analysing the graph, the function falls to the left and rises to the right
Chapter 2 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
- A cylindrical chemical storage tank with a capacity of 950m3 is going to be constructed in a warehouse that is 11m by 14m with a height of 10m. The specifications call for the case to be made of sheet metal that costs $90/m2, the top to be made from sheet metal that costs $45/m2 and the wall to be made of sheet metal that costs $80/m2. If you want to minimize the cost to make the storage house, how much would you end up spending to build the tank?arrow_forwardCalculate the max value of the directional derivatearrow_forwardCalculus III May I please have the example, definition semicolons, and all blanks completed and solved? Thank you so much,arrow_forward
- A company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x) = 12,000 In (0.02x+1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 80 doghouses have already been sold. The revenue will increase by $ if one more doghouse is made. (Round to the nearest cent as needed.)arrow_forwardThe population of bacteria (in millions) in a certain culture x hours after an experimental 20x nutrient is introduced into the culture is P(x) = - 2 Use the differential to approximate the changes in population for the following changes in x. 8+x a. 1 to 1.5 b. 3 to 3.25 a. Use the differential to approximate the change in population for x=1 to 1.5. Between 1 and 1.5 hours, the population of bacteria changes by million. (Round to three decimal places as needed.)arrow_forwardThe demand for grass seed (in thousands of pounds) at price p dollars is given by the following function. D(p) 3p³-2p² + 1460 Use the differential to approximate the changes in demand for the following changes in p. a. $4 to $4.11 b. $6 to $6.19arrow_forward
- Let the region R be the area enclosed by the function f(x) = 3 ln (x) and g(x) = 3 x + 1. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. Answer Attempt 1 out of 2 y 7 10 6 5 4 3 2 -1 2 3 4 5 6 x2 dx x1 = x2 = x1 Y1 = Y2 = Y1 dyarrow_forwardA manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.3x² + 7,000. How fast is the cost per month changing when production is changing at the rate of 14 units per month and the production level is 80 units? Costs are increasing at the rate of $ (Round to the nearest dollar as needed.) per month at this production level.arrow_forwarddy Assume x and y are functions of t. Evaluate for 2xy -3x+2y³ = - 72, with the conditions dt dx dt = -8, x=2, y = -3. dy dt (Type an exact answer in simplified form.)arrow_forward
- Consider the sequence below: 1 1 1 (a) Express this sequence as a recurrence relation (b) Express this sequence in the form {a}=1 (c) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 1 1 1 1, 4' 9' 16' (a) Express this sequence in the form {ak}=1 (b) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 345 2. 4' 9' 16' ·} (a) Express this sequence in the form {a}1 (b) Does this sequence converge or diverge? Justify your answer.arrow_forwardUse the growth rate of sequences theorem to find the limit or state it divergesarrow_forwardcalculate the maximum value of the directional derivativearrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





