Chapter 2.8, Problem 71E

Solution

To find: The vertical asymptotes and intercepts of the given rational function.

The vertical asymptotes are equal to $x=3$ and $x=-1$ and the $y-$ intercept is $\frac{4}{3}$ and the $x-$ intercepts are $-2,1$ .

Given information:

Consider the given function.

  $f\left(x\right)=\frac{\left(x-1\right){\left(x+2\right)}^2}{\left(x-3\right)\left(x+1\right)}$

Calculation:

To find the vertical asymptotes, set the denominator equal to zero and solve for $x$ :

  $\left(x-3\right)\left(x+1\right)=0$

This is already factored, so set each factor to zero and solve:

  $\begin{array}{c}x-3=0\text{or}x+1=0\\ x=3\text{or}x=-1\end{array}$

Since the asymptotes are line, they are written as equations of lines.

The vertical asymptotes are $x=3$ and $x=-1$ .

Now, find the intercepts of the given function.

For the $y-$ intercepts, substitute $x=0$ :

  $\begin{array}{c}f\left(x\right)=\frac{\left(0-1\right){\left(0+2\right)}^2}{\left(0-3\right)\left(0+1\right)}\\ y=\frac{\left(-1\right){\left(2\right)}^2}{\left(-3\right)\left(1\right)}\\ y=\frac{4}{3}\end{array}$

For the $x-$ intercepts, substitute $f\left(x\right)=0$ :

  $\begin{array}{c}0=\frac{\left(x-1\right){\left(x+2\right)}^2}{\left(x-3\right)\left(0+1\right)}\\ \left(x-1\right){\left(x+2\right)}^2=0\\ x-1=0\text{or}{\left(x+2\right)}^2=0\\ x=1\text{or}x+2=0\\ x=1\text{or}x=-2\end{array}$

Therefore, the $y-$ intercept is $\frac{4}{3}$ and the $x-$ intercepts are $-2,1$ .

Now, using the sign chart and make a table of values to the draw the graph of the function.

First find the boundary points of the function $f\left(x\right)$ .

To set numerator and the denominator equal to zero. These are the values that make the quotient zero or undefined and solve for $x$ :

  $\begin{array}{c}\left(x-1\right){\left(x+2\right)}^2=0\\ x=-2,1\end{array}$

And

  $\begin{array}{c}\left(x-3\right)\left(x+1\right)=0\\ x=-1,3\end{array}$

So, the boundary points of the function $f\left(x\right)$ are $-2,-1,1,3$ .

Now, locate these zeros on the number line (or sign chart) and dividing the number line into intervals and check the function $f\left(x\right)$ is positive or negative at each interval below:

  

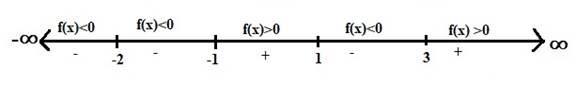
Now, make a table for the function $f\left(x\right)$ and $x$ below:

$x$	$f\left(x\right)$
$-10$	$-\frac{704}{117}$
$-2$	$0$
$0$	$\frac{4}{3}$
$1$	$0$
$2$	$-\frac{16}{3}$
$4$	$\frac{108}{5}$
$10$	$\frac{1296}{77}$

Now, draw the graph with help of above table:

  

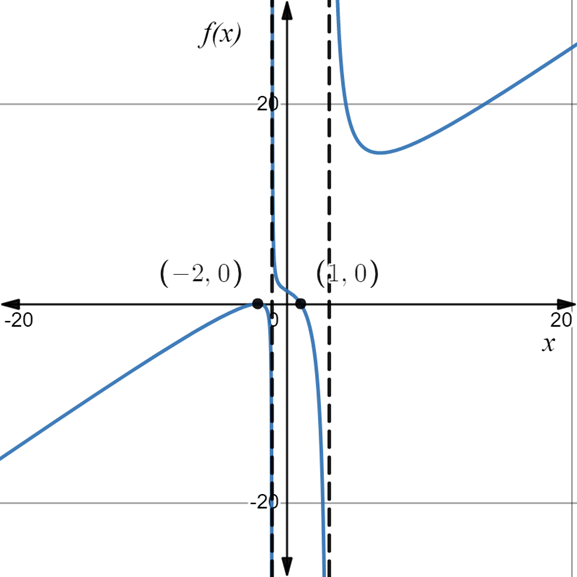
Hence, the vertical asymptotes are $x=3$ and $x=-1$ and the $y-$ intercept is $\frac{4}{3}$ and the $x-$ intercepts are $-2,1$ .